Question

有编号为1，2，3，…，n的n个学生，入坐编号为1，2，3，…n的n个座位．每个学生规定坐一个座位，设学生所坐的座位号与该生的编号不同的学生人数为ξ，已知ξ=2时，共有6种坐法．
（1）求n的值；
（2）求随机变量ξ的概率分布列和数学期望．

Answer 1

分析：（1）解题的关键是ξ=2时，共有6种坐法，写出关于n的表示式，解出未知量，把不合题意的舍去．
（2）学生所坐的座位号与该生的编号不同的学生人数为ξ，由题意知ξ的可能取值是0，2，3，4，当变量是0时表示学生所坐的座位号与该生的编号都相同，当变量是2时表示学生所坐的座位号与该生的编号有2个相同，理解变量对应的事件，写出分布列和期望．

解答：解：（1）∵当ξ=2时，有C_n²种坐法，
∴C_n²=6，
即

n(n-1)

2

=6，
n2-n-12=0，n=4或n=-3（舍去），
∴n=4．

（2）∵学生所坐的座位号与该生的编号不同的学生人数为ξ，
由题意知ξ的可能取值是0，2，3，4，
当变量是0时表示学生所坐的座位号与该生的编号都相同，
当变量是2时表示学生所坐的座位号与该生的编号有2个相同，
当变量是3时表示学生所坐的座位号与该生的编号有1个相同，
当变量是4时表示学生所坐的座位号与该生的编号有0个相同，
∴P(ξ=0)=

1

A 4 4

=

1

24

，
P(ξ=2)=

C 2 4 ×1

A 4 4

=

6

24

=

1

4

，
P(ξ=3)=

C 3 4 ×2

A 4 4

=

8

24

=

1

3

，
P(ξ=4)=

9

24

=

3

8

，
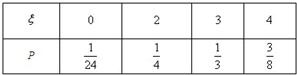
∴ξ的概率分布列为：

∴Eξ=0×

1

24

+2×

1

4

+3×

1

3

+4×

3

8

=3．

点评：培养运用从具体到抽象、从特殊到一般的观点分析问题的能力，充分体现数学的化归思想．启发诱导的同时，训练了学生观察和概括归纳的能力．