
分析 (Ⅰ)根据已知设椭圆的焦距2c,当y=c时,|MN|=|x1-x2|=$\frac{2{b}^{2}}{a}$,由题意得,△MNF2的面积为$\frac{1}{2}×$|MN|×|F1F2|=c|MN|=$\frac{2{b}^{2}c}{a}=\sqrt{3}$,又∵$\frac{c}{a}=\frac{\sqrt{3}}{2}$,解得a、b即可.
(Ⅱ)设A(x1,y1),B(x2,y2),P(0,y0),分类讨论:当m=0时,利用椭圆的对称性即可得出;m≠0时,直线AB的方程与椭圆的方程联立得到△>0及根与系数的关系,再利用向量相等,代入计算即可得出.
解答 解:(Ⅰ)根据已知设椭圆的焦距2c,当y=c时,|MN|=|x1-x2|=$\frac{2{b}^{2}}{a}$,
由题意得,△MNF2的面积为$\frac{1}{2}×$|MN|×|F1F2|=c|MN|=$\frac{2{b}^{2}c}{a}=\sqrt{3}$,
又∵$\frac{c}{a}=\frac{\sqrt{3}}{2}$,解得b2=1,a2=4,
椭圆C的标准方程为:x2+$\frac{{y}^{2}}{4}=1$.
(Ⅱ)当m=0时,则P(0,0),由椭圆的对称性得$\overrightarrow{AP}=\overrightarrow{PB},即\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{0}$,
∴m=0时,存在实数λ,使得$\overrightarrow{OA}$+λ$\overrightarrow{OB}$=4$\overrightarrow{OP}$,
当m≠0时,由$\overrightarrow{OA}$+λ$\overrightarrow{OB}$=4$\overrightarrow{OP}$,得$\overrightarrow{OP}=\frac{1}{4}\overrightarrow{OA}+\frac{λ}{4}\overrightarrow{OB}$,
∵A、B、p三点共线,∴1+λ=4,⇒λ=3⇒$\overrightarrow{AP}=3\overrightarrow{PB}$
设A(x1,y1),B(x2,y2)
由$\left\{\begin{array}{l}{y=kx+m}\\{4{x}^{2}+{y}^{2}-4=0}\end{array}\right.$,得(k2+4)x2+2mkx+m2-4=0,
由已知得△=4m2k2-4(k2+4)(m2-4)>0,即k2-m2+4>0
且x1+x2=$\frac{-2km}{{k}^{2}+4}$,x1x2=$\frac{{m}^{2}-4}{{k}^{2}+4}$.
由$\overrightarrow{AP}=3\overrightarrow{PB}$得x1=-3x2
3(x1+x2)2+4x1x2=0,∴$\frac{12{k}^{2}{m}^{2}}{({k}^{2}+4)^{2}}+\frac{4({m}^{2}-4)}{{k}^{2}+4}=0$,⇒m2k2+m2-k2-4=0
显然m2=1不成立,∴${k}^{2}=\frac{4-{m}^{2}}{{m}^{2}-1}$
∵k2-m2+4>0,∴$\frac{4-{m}^{2}}{{m}^{2}-1}-{m}^{2}+4>0$,即$\frac{(4-{m}^{2}){m}^{2}}{{m}^{2}-1}>0$.
解得-2<m<-1或1<m<2.
综上所述,m的取值范围为(-2,-1)∪(1,2)∪{0}
点评 本题考查椭圆的标准方程的求法,考查了椭圆的简单性质、涉及直线与椭圆相交问题,常转化为关于x的一元二次方程,利用△>0及根与系数的关系、向量相等等基础知识与基本技能方法求解,考查了推理能力和计算能力,属于中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
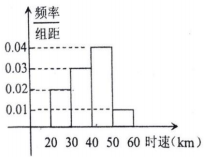 太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )
太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )| A. | 30辆 | B. | 35辆 | C. | 40辆 | D. | 50辆 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{4}$ | B. | $\frac{13}{4}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,ex≤x+1 | B. | ?x≤0,ex>x+1 | C. | ?x>0,ex≤x+1 | D. | ?x>0,ex≤x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com