
【题目】已知![]() ,
,![]() 是函数
是函数![]() 的两个零点,其中常数
的两个零点,其中常数![]() ,
,![]() ,设
,设![]() .
.
(Ⅰ)用![]() ,
,![]() 表示
表示![]() ,
,![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求证:对任意的![]() .
.
【答案】(Ⅰ)![]()
![]() (Ⅱ)详见解析,(Ⅲ)详见解析.
(Ⅱ)详见解析,(Ⅲ)详见解析.
【解析】
试题(Ⅰ)由题意得:![]() ,
,![]() .因为
.因为![]() ,所以
,所以![]() .
.![]() .对抽象的求和符号具体化处理,是解答本题的关键.(Ⅱ)
.对抽象的求和符号具体化处理,是解答本题的关键.(Ⅱ)![]() 而
而![]()
![]()
![]() ,(Ⅲ)用数学归纳法证明有关自然数的命题. (1)当
,(Ⅲ)用数学归纳法证明有关自然数的命题. (1)当![]() 时,由(Ⅰ)问知
时,由(Ⅰ)问知![]() 是整数,结论成立.(2)假设当
是整数,结论成立.(2)假设当![]()
![]() (
(![]() )时结论成立,即
)时结论成立,即![]() 都是整数,由(Ⅱ)问知
都是整数,由(Ⅱ)问知![]() .即
.即![]() 时,结论也成立.
时,结论也成立.
解:(Ⅰ)由![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
![]() . 3分
. 3分
(Ⅱ)由![]() ,得
,得
![]() .
.
即![]() ,同理,
,同理,![]() .
.
所以![]() .
.
所以![]() . 8分
. 8分
(Ⅲ)用数学归纳法证明.
(1)当![]() 时,由(Ⅰ)问知
时,由(Ⅰ)问知![]() 是整数,结论成立.
是整数,结论成立.
(2)假设当![]()
![]() (
(![]() )时结论成立,即
)时结论成立,即![]() 都是整数.
都是整数.
由![]() ,得
,得![]() .
.
即![]() .
.
所以![]() ,
,![]() .
.
所以![]() .
.
即![]() .
.
由![]() 都是整数,且
都是整数,且![]() ,
,![]() ,所以
,所以![]() 也是整数.
也是整数.
即![]() 时,结论也成立.
时,结论也成立.
由(1)(2)可知,对于一切![]() ,
,![]() 的值都是整数. 13分
的值都是整数. 13分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中![]() 浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化
浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化![]() 年除夕18时和初一2时,国家环保部门对8个城市空气中
年除夕18时和初一2时,国家环保部门对8个城市空气中![]() 浓度监测的数据如表
浓度监测的数据如表![]() 单位:微克
单位:微克![]() 立方米
立方米![]() .
.
除夕18时 | 初一2时 | |
北京 | 75 | 647 |
天津 | 66 | 400 |
石家庄 | 89 | 375 |
廊坊 | 102 | 399 |
太原 | 46 | 115 |
上海 | 16 | 17 |
南京 | 35 | 44 |
杭州 | 131 | 39 |
![]() Ⅰ
Ⅰ![]() 求这8个城市除夕18时空气中
求这8个城市除夕18时空气中![]() 浓度的平均值;
浓度的平均值;
![]() Ⅱ
Ⅱ![]() 环保部门发现:除夕18时到初一2时空气中
环保部门发现:除夕18时到初一2时空气中![]() 浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹
浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹![]() 从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
![]() Ⅲ
Ⅲ![]() 记2017年除夕18时和初一2时以上8个城市空气中
记2017年除夕18时和初一2时以上8个城市空气中![]() 浓度的方差分别为
浓度的方差分别为![]() 和
和![]() ,比较
,比较![]() 和
和![]() 的大小关系
的大小关系![]() 只需写出结果
只需写出结果![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的55名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | ||
男生 | 20 | 5 | |
女生 | 10 | 20 | |
(1)判断是否有99.5%的把握认为喜欢“应用统计”课程与性别有关?
(2)用分层抽样的方法从喜欢统计课程的学生中抽取6名学生作进一步调查,将这6名学生作为一个样本,从中任选2人,求恰有1个男生和1个女生的概率.
临界值参考:
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,
,![]() 为抛物线上在第一象限内一点,
为抛物线上在第一象限内一点,![]() 为原点,
为原点,![]() 面积为
面积为![]() .
.
(1)求抛物线方程;
(2)过![]() 点作两条直线分别交抛物线于异于点
点作两条直线分别交抛物线于异于点![]() 的两点
的两点![]() ,
,![]() ,且两直线斜率之和为
,且两直线斜率之和为![]() ,
,
(i)若![]() 为常数,求证直线
为常数,求证直线![]() 过定点
过定点![]() ;
;
(ii)当![]() 改变时,求(i)中距离
改变时,求(i)中距离![]() 最近的点
最近的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,底面ABCD为直角梯形,AD//BC,∠SAD =∠DAB=![]() ,SA=3,SB=5,
,SA=3,SB=5,![]() ,
,![]() ,
,![]() .
.
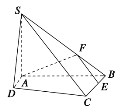
(1)求证:AB![]() 平面SAD;
平面SAD;
(2)求平面SCD与平面SAB所成的锐二面角的余弦值;
(3)点E,F分别为线段BC,SB上的一点,若平面AEF//平面SCD,求三棱锥B-AEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 四所高校中选2所.
四所高校中选2所.
(Ⅰ)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(Ⅱ)若已知甲同学特别喜欢![]() 高校,他必选
高校,他必选![]() 校,另在
校,另在![]() 三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
三校中再随机选1所;而同学乙和丙对四所高校没有偏爱,因此他们每人在四所高校中随机选2所.
(ⅰ)求甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率;
高校的概率;
(ⅱ)记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 校的人数,求随机变量
校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 与直线
与直线![]() 相切,点A为圆
相切,点A为圆![]() 上一动点,
上一动点,![]() 轴于点N,且动点满足
轴于点N,且动点满足![]() ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)设P,Q是曲线C上两动点,线段![]() 的中点为T,
的中点为T,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为直角梯形,BC∥AD,∠BAD=90°,BC=2,AD=3,四边形ABEF为平行四边形,AB=1,BE=2,∠EBA=60°,平面ABEF⊥平面ABCD.
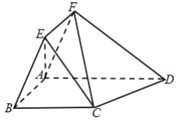
(1)求证:AE⊥平面ABCD;
(2)求平面ABEF与平面FCD所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com