
【题目】在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=BC=CA=2![]() ,AA1=4,D为A1B1的中点,E为棱BB1上的点,AB1⊥平面C1DE,且B1,C1,D,E四点在同一球面上,则该球的表面积为( )
,AA1=4,D为A1B1的中点,E为棱BB1上的点,AB1⊥平面C1DE,且B1,C1,D,E四点在同一球面上,则该球的表面积为( )
A. 9π B. 11π C. 12π D. 14π
【答案】A
【解析】
由题意,AA1⊥平面ABC,三棱柱ABC﹣A1B1C1是直三棱柱,AB=BC=CA=2![]() ,底面是正的三角形.D为A1B1的中点,E为棱BB1上的点,AB1⊥平面C1DE,求E为棱BB1上的位置,在求解B1﹣C1DE三棱锥的外接球即可得球的表面积.
,底面是正的三角形.D为A1B1的中点,E为棱BB1上的点,AB1⊥平面C1DE,求E为棱BB1上的位置,在求解B1﹣C1DE三棱锥的外接球即可得球的表面积.
由题意,AA1⊥平面ABC,三棱柱ABC﹣A1B1C1是直三棱柱,
AB=BC=CA=2![]() ,底面是正三角形.
,底面是正三角形.
AB1![]() ,∴sin∠AB1B
,∴sin∠AB1B![]() .
.
那么DB1![]() ,
,
AB1⊥平面C1DE,AB1⊥DE,D为A1B1的中点,E为棱BB1上的点,
DE∩AB1=M,
∵△ABB1∽△EB1M
∴![]()
那么:EB1=1
则在D﹣B1C1E三棱锥中:B1C1=2![]() ,C1D
,C1D![]() ,EC1=3,DE
,EC1=3,DE![]() ,B1D
,B1D![]()
∵EB1⊥平面DB1C1,
底面DB1C1是直角三角形,
∴球心在EC1在的中点上,
∴R![]()
球的表面积S=4πR2=9π.
故选:A.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,曲线C1: ![]() (θ为参数),在以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系中,曲线C2:ρsin(
(θ为参数),在以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系中,曲线C2:ρsin( ![]() )=1.
)=1.
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)曲线C1上恰好存在三个不同的点到曲线C2的距离相等,分别求这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点![]() 在正视图中所示位置:
在正视图中所示位置:![]() 为所在线段中点,
为所在线段中点,![]() 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从![]() 点到
点到![]() 点的最短路径的长.
点的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣a(x﹣1)(a∈R)
(1)若函数f(x)在x=0处有极值,求a的值及f(x)的单调区间
(2)若存在实数x0∈(0, ![]() ),使得f(x0)<0,求实数a的取值范围.
),使得f(x0)<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据(xi , yi)(i=1,2,…,6),如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
已知 ![]() =80.
=80.
(Ⅰ)求出q的值;
(Ⅱ)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程 ![]() ;可供选择的数据:
;可供选择的数据: ![]() ,
, ![]()
(Ⅲ)用 ![]() 表示用(Ⅱ)中所求的线性回归方程得到的与xi对应的产品销量的估计值.当销售数据(xi , yi)对应的残差的绝对值
表示用(Ⅱ)中所求的线性回归方程得到的与xi对应的产品销量的估计值.当销售数据(xi , yi)对应的残差的绝对值 ![]() 时,则将销售数据(xi , yi)称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数ξ的分布列和数学期望E(ξ).
时,则将销售数据(xi , yi)称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数ξ的分布列和数学期望E(ξ).
(参考公式:线性回归方程中 ![]() ,
, ![]() 的最小二乘估计分别为
的最小二乘估计分别为 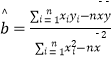 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin( ![]() +x)(cosx﹣2sinx)+sin2x的图象向左平移
+x)(cosx﹣2sinx)+sin2x的图象向左平移 ![]() 个单位长度后得到函数g(x),则g(x)具有性质( )
个单位长度后得到函数g(x),则g(x)具有性质( )
A.在(0, ![]() )上单调递增,为奇函数
)上单调递增,为奇函数
B.周期为π,图象关于( ![]() )对称
)对称
C.最大值为 ![]() ,图象关于直线x=
,图象关于直线x= ![]() 对称
对称
D.在(﹣ ![]() )上单调递增,为偶函数
)上单调递增,为偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2
(t为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2 ![]() cos(
cos( ![]() +θ).
+θ).
(I)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于M,N两点,求|MN|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com