
【题目】某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.
(1)用十位数为茎,在答题卡中画出原始数据的茎叶图;
(2)用分层抽样的方法在乙运动员得分十位数为 2,3,4 的比赛中抽取一个容量为 5 的样本,从该样本中随机抽取 2 场,求其中恰有 1 场得分大于 40 分的概率.
科目:高中数学 来源: 题型:
【题目】如图,ABCD﹣A1B1C1D1为正方体,则以下结论:①BD∥平面CB1D1;②AC1⊥BD;③AC1⊥平面CB1D1其中正确结论的个数是( )
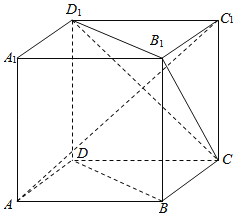
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)设数列![]() 的前
的前![]() 项和为
项和为![]() .已知
.已知![]() ,
, ![]() ,
, ![]() .
.
(1)写出![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(2)记![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() ;
;
(3)若数列![]() 满足
满足![]() ,
, ![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
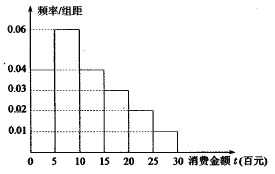
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:
(1)求网民消费金额![]() 的平均值和中位数
的平均值和中位数![]() ;
;
(2)把下表中空格里的数填上,能否有![]() 的把握认为网购消费与性别有关;
的把握认为网购消费与性别有关;
男 | 女 | 合计 | |
| |||
| 30 | ||
合计 | 45 |
附表:
|
|
|
|
|
|
|
|
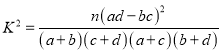 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:

(1)试问这3年的前7个月中哪个月的平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份 | 1 | 2 | 3 | 4 |
利润 | 4 | 4 | 6 | 6 |
相关公式:  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是


A. A B. B C. C D. D
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为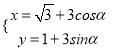 (
(![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为非负半轴为极轴建立极坐标系.
轴为非负半轴为极轴建立极坐标系.
(1)求圆![]() 的普通方程与极坐标方程;
的普通方程与极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,求圆
,求圆![]() 上的点到直线
上的点到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中![]() 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)由直线![]() 上一点向曲线
上一点向曲线![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com