
分析 根据斜二测画法,建立适当的坐标系,画出对应平面图形的直观图即可.
解答 解:(1)画出△ABC,建立直角坐标系xoy,如图所示;
再作出坐标系x′O′y′,使∠x′O′y′=45°,
在x′轴上作线段A′B′=AB,
则y′轴上分别作线段O′C′=$\frac{1}{2}$OC,
连结A′C′,B′C′,即为△ABC的直观图,如图1所示;
(2)画出?ABCD,建立直角坐标系xoy,如图所示;
再作出坐标系x′O′y′,使∠x′O′y′=45°,
在x′轴上作线段O′B′=OB,O′A′=OA,
在y′轴上作线段O′D′=$\frac{1}{2}$OD,
过D′作D′C′∥O′B′,使D′C′=DC,
连接A′B′C′D′,即为?ABCD的直观图,如图2;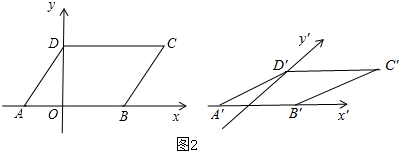
(3)画出正八边形OABCDEFG,建立直角坐标系xoy,如图所示;
再作出坐标系x′O′y′,使∠x′O′y′=45°,
在x′轴上作线段O′A′=OA,
在y′轴上作线段O′E′=$\frac{1}{2}$OE,
过E′作E′D′∥O′A′,使E′D′=ED,
再按照斜二测画法画出点B、C、F、G的对应点B′、C′、E′、G′,
连接A′B′C′D′E′F′G′O′,即得正八边形OABCDEFG的直观图,如图3;
点评 本题考查了用斜二测画法画平面图形的直观图的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或x>2} | B. | {x|x<-2或x>4} | C. | {x|x<0或x>6} | D. | {x|x<1或x>5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,4) | B. | [-1,4) | C. | [0,1,2,3] | D. | [1,2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com