
【题目】定义在R上的奇函数f(x),当x≥0时,f(x)= ![]() ,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
A.3a﹣1
B.1﹣3a
C.3﹣a﹣1
D.1﹣3﹣a
【答案】B
【解析】解:∵定义在R上的奇函数f(x), ∴f(﹣x)=﹣f(x),
∵当x≥0时,f(x)= ![]() ,
,
∴当x≥0时,f(x)= 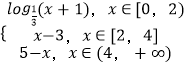 ,
,
得出x<0时,f(x)= ![]()
画出图象得出: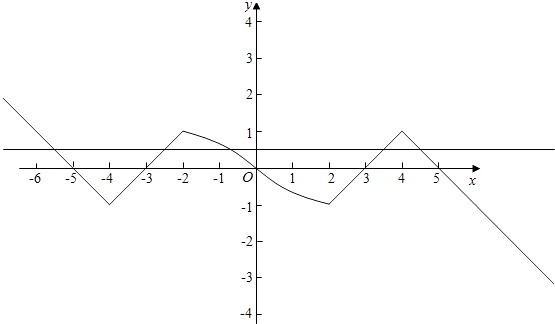
如图从左向右零点为x1 , x2 , x3 , x4 , x5 ,
根据对称性得出:x1+x2=﹣4×2=﹣8,
x4+x5=2×4=8,﹣log ![]() (﹣x3+1)=a,x3=1﹣3a ,
(﹣x3+1)=a,x3=1﹣3a ,
故x1+x2+x3+x4+x5=﹣8+1﹣3a+8=1﹣3a ,
故选:B
【考点精析】掌握函数的零点与方程根的关系是解答本题的根本,需要知道二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是____________.
【答案】![]()
【解析】∵圆C的方程可化为(x-4)2+y2=1,∴圆C的圆心为(4,0),半径为1.由题意知,直线y=kx-2上至少存在一点A(x0,kx0-2),以该点为圆心,1为半径的圆与圆C有公共点,∴存在x0∈R,使得AC≤1+1成立,即ACmin≤2.
∵ACmin即为点C到直线y=kx-2的距离![]() ,
,
∴![]() ≤2,解得0≤k≤
≤2,解得0≤k≤![]() .∴k的最大值是
.∴k的最大值是![]() .
.
【题型】填空题
【结束】
15
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() .
.
(1)若直线![]() 与直线
与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(2)若![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,已知
上,已知![]() 的中点在
的中点在![]() 轴上,求点
轴上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究函数f(x)= ![]() 的性质,完成下面两个问题:
的性质,完成下面两个问题:
①将f(2),f(3),f(5)按从小到大排列为;
②函数g(x)= ![]() (x> 0)的最大值为 .
(x> 0)的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥 ![]() 的底面
的底面 ![]() 为正方形,
为正方形, ![]() ⊥底面
⊥底面 ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() .
.
(Ⅰ)求证 ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角;
所成的角;
(Ⅲ)求四棱锥 ![]() 的外接球的体积.
的外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体中, ![]() 菱形,
菱形, ![]() 是矩形,
是矩形, ![]() ⊥平面
⊥平面 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)异面直线 ![]() 与
与 ![]() 所成的角余弦值;
所成的角余弦值;
(Ⅱ)求证平面 ![]() ⊥平面
⊥平面 ![]() ;
;
(Ⅲ)在线段 ![]() 取一点
取一点 ![]() ,当二面角
,当二面角 ![]() 的大小为60°时,求
的大小为60°时,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图圆柱高为 ![]() ,半径为
,半径为 ![]() ,不计厚度,单位:米),按计划容积为
,不计厚度,单位:米),按计划容积为 ![]() 立方米,且
立方米,且 ![]() ,假设建造费用仅与表面积有关(圆柱底部不计 ),已知圆柱部分每平方米的费用为2千元,半球部分每平方米的费用为2千元,设该容器的建造费用为y千元.
,假设建造费用仅与表面积有关(圆柱底部不计 ),已知圆柱部分每平方米的费用为2千元,半球部分每平方米的费用为2千元,设该容器的建造费用为y千元.
(1)求y关于r的函数关系,并求其定义域;
(2)求建造费用最小时的 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 的部分图象如图所示.
的部分图象如图所示.
(1)求函数![]() 的解析式;
的解析式;
(2)将![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 图象的一个对称轴为
图象的一个对称轴为![]() ,求
,求![]() 的最小值;
的最小值;
(3)在第(2)问的前提下,求函数![]() 在
在![]() 上的单调区间.
上的单调区间.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE. 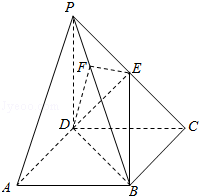
(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若面DEF与面ABCD所成二面角的大小为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com