【题目】6男4女站成一排,求满足下列条件的排法共有多少种.(列出算式即可)
(1)任何2名女生都不相邻,有多少种排法?
(2)男甲不在首位,男乙不在末位,有多少种排法?
(3)男生甲、乙、丙顺序一定,有多少种排法?
(4)男甲在男乙的左边(不一定相邻)有多少种不同的排法?
【答案】（1）
；（2）
；（3）
；（4）
【解析】
（1）任何两个女生都不得相邻，利用插空法，问题得以解决，
（2）男甲不在首位，男乙不在末位，利用间接法，故问题得以解决，
（3）男生甲、乙、丙顺序一定，利用定序法，问题得以解决．
（4）由于男甲要么在男乙的左边，要么在男乙的右边，故利用除法可得结论．
(1)任何2名女生都不相邻,则把女生插空,所以先排男生再让女生插到男生的空中,共有
·
种不同排法.
(2)甲在首位的排法共有
种,乙在末位的排法共有种,甲在首位且乙在末位的排法有
种,因此共有(
-2+)种排法.
(3)10人的所有排列方法有种,其中甲、乙、丙的排序有
种,其中只有一种符合题设要求,所以甲、乙、丙顺序一定的排法有
种.
(4)男甲在男乙的左边的10人排列与男甲在男乙的右边的10人排列数相等,而10人排列数恰好是这二者之和,因此满足条件的有
种排法.
口算心算速算应用题系列答案
同步拓展阅读系列答案科目：高中数学 来源： 题型：
【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c．已知asinA=4bsinB，ac= 
（a2﹣b2﹣c2）．（13分）
（Ⅰ）求cosA的值；
（Ⅱ）求sin（2B﹣A）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设等差数列{an}的前n项和为Sn ， 且S4=4S2 ， a2+a4=10．
（1）求数列{an}通项公式；
（2）若数列{bn}满足 
+ 
+…+ 
=1﹣ 
，n∈N* ， 求数列{bn}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
，直线
与E交于A、B两点，且
，其中O为原点.
（1）求抛物线E的方程；
（2）点C坐标为
，记直线CA、CB的斜率分别为
，证明： 
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
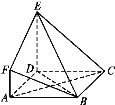
(1)求二面角F-BE-D的余弦值;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
