
【题目】记max{x,y}= ![]() ,min{x,y}=
,min{x,y}= ![]() ,设
,设 ![]() ,
, ![]() 为平面向量,则( )
为平面向量,则( )
A.min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}≤min{|
|}≤min{| ![]() |,|
|,| ![]() |}
|}
B.min{| ![]() +
+ ![]() |,|
|,| ![]() ﹣
﹣ ![]() |}≥min{|
|}≥min{| ![]() |,|
|,| ![]() |}
|}
C.max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}≤|
|2}≤| ![]() |2+|
|2+| ![]() |2
|2
D.max{| ![]() +
+ ![]() |2 , |
|2 , | ![]() ﹣
﹣ ![]() |2}≥|
|2}≥| ![]() |2
|2
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() , g(x)=ex+m , 其中e=2.718….
, g(x)=ex+m , 其中e=2.718….
(1)求f(x)在x=1处的切线方程;
(2)当m≥﹣2时,证明:f(x)<g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示四棱锥![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.

![]() 求四棱锥
求四棱锥![]() 的体积;
的体积;
![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() 在棱
在棱![]() 上是否存在点
上是否存在点![]() 异于点
异于点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某二手车交易市场对某型号的二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程:(参考公式:
的回归直线方程:(参考公式: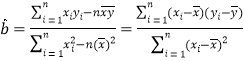 ,
, ![]() .)
.)
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:
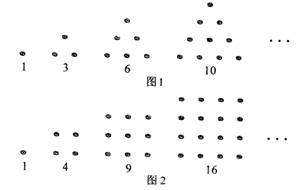
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
A. 36 B. 45 C. 99 D. 100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥A﹣BCD及其侧视图、俯视图如图所示,设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP. 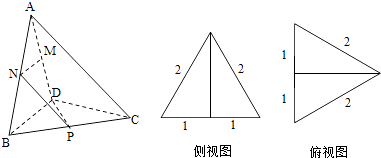
(1)证明:P是线段BC的中点;
(2)求二面角A﹣NP﹣M的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com