
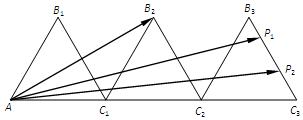
 如图,△AB1C1,△C1B2C2,△C2B3C3是三个边长为2的等边三角形,且有一条边在同一直线上,边B3C3上有2个不同的点P1,P2,则$\overrightarrow{A{B_2}}•(\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}})$=36.
如图,△AB1C1,△C1B2C2,△C2B3C3是三个边长为2的等边三角形,且有一条边在同一直线上,边B3C3上有2个不同的点P1,P2,则$\overrightarrow{A{B_2}}•(\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}})$=36. 分析 根据图形证明$\overrightarrow{{AB}_{2}}$⊥$\overrightarrow{{{B}_{3}C}_{3}}$,$\overrightarrow{{AB}_{2}}$•$\overrightarrow{{{C}_{3}B}_{3}}$=0;根据平面向量的线性表示与数量积运算计算$\overrightarrow{A{B_2}}•(\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}})$即可.
解答 解:由图可知,∠B2AC3=30°,又∠AC2B2=60°,
∴$\overrightarrow{{AB}_{2}}$⊥$\overrightarrow{{{B}_{2}C}_{2}}$,
又$\overrightarrow{{{B}_{2}C}_{2}}$∥$\overrightarrow{{{B}_{3}C}_{3}}$,
∴$\overrightarrow{{AB}_{2}}$⊥$\overrightarrow{{{B}_{3}C}_{3}}$,
∴$\overrightarrow{{AB}_{2}}$•$\overrightarrow{{{C}_{3}B}_{3}}$=0;
∴$\overrightarrow{A{B_2}}•(\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}})$=$\overrightarrow{{AB}_{2}}$•[($\overrightarrow{{AC}_{3}}$+$\overrightarrow{{{C}_{3}P}_{1}}$)+($\overrightarrow{{AC}_{3}}$+$\overrightarrow{{{C}_{3}P}_{2}}$)]
=$\overrightarrow{{AB}_{2}}$•$\overrightarrow{{AC}_{3}}$+$\overrightarrow{{AB}_{2}}$•m$\overrightarrow{{{C}_{3}B}_{3}}$+$\overrightarrow{{AB}_{2}}$•$\overrightarrow{{AC}_{3}}$+$\overrightarrow{{AB}_{2}}$•n$\overrightarrow{{{C}_{3}B}_{3}}$
=2$\overrightarrow{{AB}_{2}}$•$\overrightarrow{{AC}_{3}}$
=2×2$\sqrt{3}$×6×cos30°
=36.
故答案为:36.
点评 本题考查了平面向量线性表示与数量积的运算问题,也考查了三角形中边角关系的运用问题,是综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,0,1} | C. | {-1,0,1,2} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年陕西省高一下学期期末考数学试卷(解析版) 题型:解答题
已知函数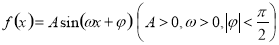 的图像过点
的图像过点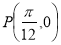 ,图像上与
,图像上与
点P最近的一个顶点是
(1)求函数的解析式;
(2)求使函数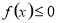 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
已知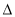 ABC的三边为a,b,c.其面积S=
ABC的三边为a,b,c.其面积S= 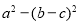 ,且b+c=8.
,且b+c=8.
(1)求cosA
(2)求S的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com