
【题目】已知定义在区间[﹣3,3]上的单调函数f(x)满足:对任意的x∈[﹣3,3],都有f(f(x)﹣2x)=6,则在[﹣3,3]上随机取一个实数x,使得f(x)的值不小于4的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() 是非零不共线的向量,设
是非零不共线的向量,设 ![]() =
= ![]()
![]() +
+ ![]()
![]() ,定义点集M={K|
,定义点集M={K| ![]() =
= ![]() },当K1 , K2∈M时,若对于任意的r≥2,不等式|
},当K1 , K2∈M时,若对于任意的r≥2,不等式| ![]() |≤c|
|≤c| ![]() |恒成立,则实数c的最小值为 .
|恒成立,则实数c的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +
+ ![]() =1,圆C2:x2+y2=t经过椭圆C1的焦点.
=1,圆C2:x2+y2=t经过椭圆C1的焦点.
(1)设P为椭圆上任意一点,过点P作圆C2的切线,切点为Q,求△POQ面积的取值范围,其中O为坐标原点;
(2)过点M(﹣1,0)的直线l与曲线C1 , C2自上而下依次交于点A,B,C,D,若|AB|=|CD|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面是以O为中心的菱形,
中,底面是以O为中心的菱形,![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,M为BC上一点.
,M为BC上一点.
![]() 当BM等于多少时,
当BM等于多少时,![]() 平面POM?
平面POM?
![]() 在满足
在满足![]() 的条件下,若
的条件下,若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在其定义域内存在
在其定义域内存在![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 为“可分拆函数”.
为“可分拆函数”.
(1)试判断函数![]() 是否为“可分拆函数”?并说明你的理由;
是否为“可分拆函数”?并说明你的理由;
(2)设函数![]() 为“可分拆函数”,求实数
为“可分拆函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】去年“十一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后,得到如图的频率分布直方图.
后,得到如图的频率分布直方图.
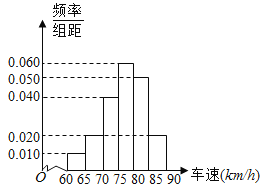
(I)调查公司在抽样时用到的是哪种抽样方法?
(II)求这40辆小型汽车车速的众数和中位数的估计值;
(III)若从这40辆车速在![]() 的小型汽车中任意抽取2辆,求抽出的2辆车车速都在
的小型汽车中任意抽取2辆,求抽出的2辆车车速都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的长轴长为6,离心率为 ![]() ,F2为椭圆的右焦点.
,F2为椭圆的右焦点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)点M在圆x2+y2=8上,且M在第一象限,过M作圆x2+y2=8的切线交椭圆于P,Q两点,判断△PF2Q的周长是否为定值并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com