
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,长轴长为
,长轴长为![]() ,直线
,直线![]() :
:![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() 、
、![]() .
.
(1)求椭圆的方程;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值(
的值(![]() 点为坐标原点);
点为坐标原点);
(3)若坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】在某次数学考试中,小江的成绩在90分以上的概率是0.25,在![]() 的概率是0.48,在
的概率是0.48,在![]() 的概率是0.11,在
的概率是0.11,在![]() 的概率是0.09,在60分以下的概率是0.07.计算:
的概率是0.09,在60分以下的概率是0.07.计算:
(1)小江在此次数学考试中取得80分及以上的概率;
(2)小江考试及格(成绩不低于60分)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且其中一个焦点的坐标为
,且其中一个焦点的坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆交于两点
与椭圆交于两点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的一次篮球定点投篮训练中,规定每人最多投![]() 次;在
次;在![]() 处每投进一球得
处每投进一球得![]() 分,在
分,在![]() 处每投进一球得
处每投进一球得![]() 分;如果前两次得分之和超过
分;如果前两次得分之和超过![]() 分即停止投篮,否则投第三次.同学在
分即停止投篮,否则投第三次.同学在![]() 处的命中率
处的命中率![]() 为
为![]() 0,在
0,在![]() 处的命中率为
处的命中率为![]() ,该同学选择先在
,该同学选择先在![]() 处投一球,以后都在
处投一球,以后都在![]() 处投,用
处投,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
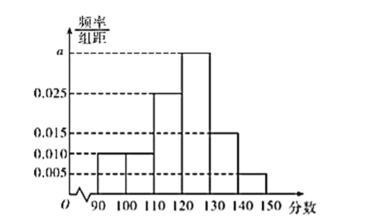
【题目】某校高二年级共有800名学生参加了数学测验(满分150分),已知这800名学生的数学成绩均不低于90分,将这800名学生的数学成绩分组如:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到的频率分布直方图如图所示,则下列说法中正确的是( )
,得到的频率分布直方图如图所示,则下列说法中正确的是( )
①![]() ;②这800名学生中数学成绩在110分以下的人数为160; ③这800名学生数学成绩的中位数约为121.4;④这800名学生数学成绩的平均数为125.
;②这800名学生中数学成绩在110分以下的人数为160; ③这800名学生数学成绩的中位数约为121.4;④这800名学生数学成绩的平均数为125.
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆W:![]() 的焦距与椭圆Ω:
的焦距与椭圆Ω:![]() +y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.
+y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.

(1)求W的标准方程:
(2)求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com