
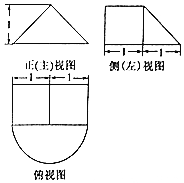
 一个由半圆锥和平放的直三棱柱(侧棱垂直于底面的三棱柱)组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半圆锥和平放的直三棱柱(侧棱垂直于底面的三棱柱)组成的几何体,其三视图如图所示,则该几何体的体积为( )| A. | 1+$\frac{π}{3}$ | B. | 1+$\frac{π}{6}$ | C. | $\frac{2}{3}$+$\frac{π}{3}$ | D. | $\frac{2}{3}$+$\frac{π}{6}$ |
分析 一个由半圆锥和平放的直三棱柱(侧棱垂直于底面的三棱柱)组成的几何体,分别求出体积,相加可得答案.
解答 解:由已知可得该几何体是一个由半圆锥和平放的直三棱柱(侧棱垂直于底面的三棱柱)组成的几何体,
三棱柱的底面如主视图所示:故底面面积为$\frac{1}{2}$×2×1=1,
棱柱的高为1,
故棱柱的体积为:1;
半圆锥的底面如俯视图中半圆所示,故底面面积为:$\frac{1}{2}π$,
半圆锥的高为:1,
故半圆锥的体积为:$\frac{1}{3}•\frac{1}{2}π•1$=$\frac{π}{6}$,
故组合体的体积V=1+$\frac{π}{6}$,
故选:D
点评 本题考查的知识点是棱柱的体积和表面积,圆锥的体积和表面积,简单几何体的三视图,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
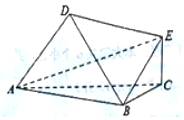 如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.
如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).| 文科生 | 理科生 | 合计 | |
| 获奖 | 5 | ||
| 不获奖 | |||
| 合计 | 200 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com