
 ijУ�Ӹ߶��꼶ѧ���������ȡ50��ѧ���������ǵ����п�����ѧ�ɼ�������100�֣��ɼ���Ϊ������40�ֵ��������ֳ����Σ�[40��50����[50��60��������[90��100]���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
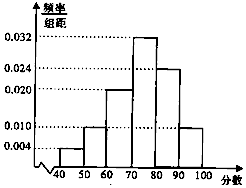
ijУ�Ӹ߶��꼶ѧ���������ȡ50��ѧ���������ǵ����п�����ѧ�ɼ�������100�֣��ɼ���Ϊ������40�ֵ��������ֳ����Σ�[40��50����[50��60��������[90��100]���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ��1������ɼ�������60����ռ��Ƶ�ʺ�Ƶ�����ɣ�
��2����������ֵ�����С���εĵױ��е㣬
������λ������Ƶ����ȣ������Ӧ��ֵ����λ����
����ÿһ��ױ��е���Զ�ӦƵ�ʣ���ͼ���ƽ��������ֵ��
��� �⣺��1���ɼ�������60����ռ��Ƶ��Ϊ��
1-��0.004+0.010����10=0.86��
���Գɼ�������60�ֵ���������ֵΪ��
1000��0.86=860���ˣ���-----------��4�֣�
��2����������ֵΪ��75��------------��6�֣�
����λ��Ϊx����x-70����0.032=0.5-0.04-0.1-0.2��
���x=75��---------��9�֣�
ƽ��������ֵΪ��
0.04��45+0.1��55+0.2��65+0.32��75+0.24��85+0.1��95=74.2��----------��12�֣�
���� ���⿼��������Ƶ�ʷֲ�ֱ��ͼ����������λ����ƽ������Ӧ�����⣬�ǻ����⣮


 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
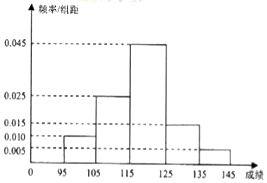 �߶���ѧICTS�����������Ժ�ijУ��95�����ϵijɼ�����ͳ�ƣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������[135��145]�����ε�����Ϊ2�ˣ�
�߶���ѧICTS�����������Ժ�ijУ��95�����ϵijɼ�����ͳ�ƣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������[135��145]�����ε�����Ϊ2�ˣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
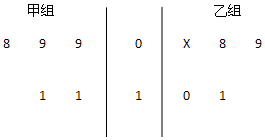 ��ͼ��Ҷͼ��¼�˼������������ͬѧ��ֲ�������������¼����һ������ģ������ȷ�ϣ���ͼ����x��ʾ
��ͼ��Ҷͼ��¼�˼������������ͬѧ��ֲ�������������¼����һ������ģ������ȷ�ϣ���ͼ����x��ʾ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
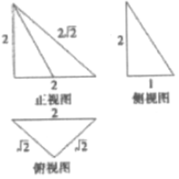
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com