
【题目】己知{an}是等差数列,其前n项和Sn=n2﹣2n+b﹣1,{bn}是等比数列,其前n项和Tn![]() ,则数列{ bn +an}的前5项和为( )
,则数列{ bn +an}的前5项和为( )
A.37B.-27C.77D.46
【答案】C
【解析】
由等差数列的求和公式、等比数列的求和公式,结合数列的递推式,可得b=1,a=2,求得数列{an},{bn}的通项公式,再由数列的分组求和,结合等差数列和等比数列的求和公式,可得所求和.
{an}是等差数列,其前n项和![]() ,
,
由等差数列的求和公式可得b﹣1=0,即b=1,
即Sn=n2﹣2n,
a1=S1=﹣1,an=Sn﹣Sn﹣1=n2﹣2n﹣(n﹣1)2+2(n﹣1)=2n﹣3,
则an=2n﹣3,n∈N*;
{bn}是等比数列,其前n项和![]() ,
,
则b1![]() 3,bn=Tn﹣Tn﹣1
3,bn=Tn﹣Tn﹣1![]() 3n
3n![]() 3n﹣1=﹣23n﹣1,
3n﹣1=﹣23n﹣1,
则![]() 3=﹣2,即a=2,
3=﹣2,即a=2,
则bn +an=n+2n,
数列{ bn +an}的前5项和为(1+2+…+5)+(2+4+…+32)
![]() 5×6
5×6![]() 77.
77.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲,乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲,乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下,计成绩不低于90分者为“成绩优秀”.

(1)从乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率;
(2)由以上统计数据填写下面2x2列联表,并判断是否有![]() 的把握认为“成绩优秀”与教学方式有关.
的把握认为“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附: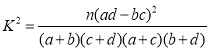
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | /tr>
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy下,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C1在变换T:
为参数),曲线C1在变换T:![]() 的作用下变成曲线C2.
的作用下变成曲线C2.
(1)求曲线C2的普通方程;
(2)若m>1,求曲线C2与曲线C3:y=m|x|-m的公共点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果无穷数列{an}的所有项恰好构成全体正整数的一个排列,则称数列{an}具有性质P.
(Ⅰ)若an![]() (k∈N*),判断数列{an}是否具有性质P,并说明理由,
(k∈N*),判断数列{an}是否具有性质P,并说明理由,
(Ⅱ)若数列{an}具有性质P,求证:{an}中一定存在三项ai,aj,ak(i<j<k)构成公差为奇数的等差数列;
(Ⅲ)若数列{an}具有性质P,则{an}中是否一定存在四项ai,aj,ak,al,(i<j<k<l)构成公差为奇数的等差数列?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)定义![]() 为
为![]() ,
,![]() 两点所在直线的斜率,若四边形
两点所在直线的斜率,若四边形![]() 为椭圆的内接四边形,且
为椭圆的内接四边形,且![]() ,
,![]() 相交于原点
相交于原点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)定义![]() 为
为![]() ,
,![]() 两点所在直线的斜率,若四边形
两点所在直线的斜率,若四边形![]() 为椭圆的内接四边形,且
为椭圆的内接四边形,且![]() ,
,![]() 相交于原点
相交于原点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且椭圆上存在一点
,且椭圆上存在一点![]() ,满足
,满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com