
分析 求出基本事件数与总数的比值即可得出结论.
解答 解:(2)∵一副除去大小王的52张扑克牌中红桃K共有1张,
∴随机抽取一张,这张牌为红桃K的概率=$\frac{1}{52}$.
(2)∵一副除去大小王的52张扑克牌中黑桃共有13张,
∴随机抽取一张,这张牌为黑桃的概率是$\frac{13}{52}$=$\frac{1}{4}$.
(3)∵一副除去大小王的52张扑克牌中抽到的数字至少大于10的共12张,
∴随机抽取一张,抽到的数字至少大于10的概率=$\frac{12}{52}$=$\frac{3}{13}$.
点评 本题考查的是概率公式,熟知随机事件A的概率P(A)=事件A可能出现的结果数所有可能出现的结果数是解答此题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
| A. | 若x>1,则?y∈(-∞,1),xy≠1 | B. | 若x=sinθcosθ,则?θ∈(0,π),x≠$\frac{1}{2}$ | ||
| C. | 若x>1,则?y∈(-∞,1),xy=1 | D. | 若x=sinθcosθ,则?θ∈(0,π),x=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{1}{x-1}$,g(x)=$\frac{x+1}{{x}^{2}-1}$ | B. | f(x)=|x+1|,g(x)=$\sqrt{{x}^{2}+2x+1}$ | ||
| C. | f(x)=x0,g(x)=1 | D. | f(x)=3x+2(x≥0),g(x)=2+3x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac>bc | B. | $\frac{b}{a}$>1 | C. | |a|>|b| | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
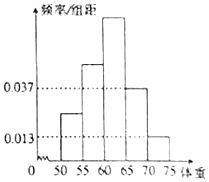 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9π,12π | B. | 12π,9π | C. | 24π,12π | D. | 15π,36π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com