练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题满分14分）
    　　已知：函数是定义在上的偶函数，当时，为实数）.
    　　（1）当时，求的解析式；
    　　（2）若，试判断上的单调性，并证明你的结论；
    　　（3）是否存在，使得当有最大值1？若存在，求出的值;若不存在，请说明理由.


    （1）
    （2）上为增函数.
    （3）存在上有最大值1.

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    在边长为4的正方形ABCD上有一点P，沿着折线BCDA由B点(起点)向A点(终点)移动，设P点移动的路程为x，△ABP的面积为y＝f(x)．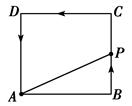

    (1)求△ABP的面积与P移动的路程间的函数关系式；
    (2)作出函数的图象，并根据图象求y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （12分）已知集合A＝{a1，a2，a3，a4}，B＝{0,1,2,3}，f是从A到B的映射．
    (1)若B中每一元素都有原象，这样不同的f有多少个？
    (2)若B中的元素0必无原象，这样的f有多少个？
    (3)若f满足f(a1)＋f(a2)＋f(a3)＋f(a4)＝4，这样的f又有多少个？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分14分）
    已知函数, 其中为常数，且函数图像过原点.
    (1)      求的值；
    (2)      证明函数在[0,2]上是单调递增函数；
    (3)      已知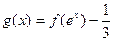函数, 求函数的零点

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分12分)
    已知函数 (∈R).
    （Ⅰ）试给出的一个值，并画出此时函数的图象；
    （Ⅱ）若函数 f (x) 在上具有单调性，求的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分分）
    已知函数.（为常数,）
    （Ⅰ）若是函数的一个极值点，求的值；
    （Ⅱ）求证：当时，在上是增函数；
    （Ⅲ）若对任意的，总存在，使不等式成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分13分)
    某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上，山脚下有一段位于水平线上笔直的公路AB，山坡面可近似地看作平面PAB，且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°＜α＜90°)，且sinα＝.现从山脚的水平公路AB某处C0开始修建一条盘山公路，该公路的第一段、第二段、第三段…，第n－1段依次为C0C1，C1C2，C2C3，…，Cn－1Cn(如图所示)，且C0C1，C1C2，C2C3，…，Cn－1Cn与AB所成的角均为β，其中0＜β＜90°，sinβ＝.试问：

    (1)每修建盘山公路多少米，垂直高度就能升高100米.若修建盘山公路至半山腰(高度为山高的一半)，在半山腰的中心Q处修建上山缆车索道站，索道PQ依山而建(与山坡面平行，离坡面高度忽略不计)，问盘山公路的长度和索道的长度各是多少？
    (2)若修建xkm盘山公路，其造价为 a万元.修建索道的造价为2a万元/km.问修建盘山公路至多高时，再修建上山索道至观景台，总造价最少.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    一块形状为直角三角形的铁皮，直角边长分别为40cm和60cm，现要将它剪成一个矩形，并以此三角形的直角为矩形的一个角，问：怎样剪，才能使剩下的残料最少?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本题满分10分)
    已知是奇函数
    ⑴、求的定义域；
    ⑵、求的值；

    查看答案和解析>>

    同步练习册答案