
【题目】如图,在三棱锥S-ABC中,∠ABC=90°,D是AC的中点,且SA=SB=SC.
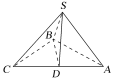
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
科目:高中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,已知点A(1,0)和点B(﹣1,0),![]() ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点.

(1)若x=![]() ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求![]() 的最小值;
的最小值;
(2)若![]() R,求
R,求![]() 的最大值及对应的x值.
的最大值及对应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,
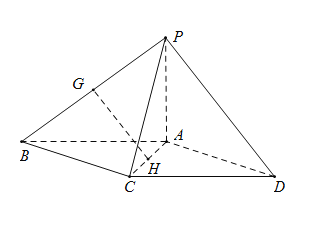
(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有( )
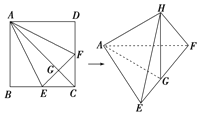
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C所对的边分别是a、b、c,且有bcosC+ccosB=2acosB.
(1)求B的大小;
(2)若△ABC的面积是![]() ,且a+c=5,求b.
,且a+c=5,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列
的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列![]() 的前n项和Sn=f(n)(n∈N*).
的前n项和Sn=f(n)(n∈N*).
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列{![]() }前n项的和Tn.
}前n项的和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com