
| A. | 0 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
分析 由函数的周期性可得f(-1)=f(1),可得k=2,再由题意可得f($\frac{17}{4}$)=f($\frac{1}{4}$)=$\frac{1}{4}$k-1,代入k值计算可得.
解答 解:∵函数周期为2,∴f(-1)=f(1),
又∵当-1≤x≤1时,f(x)=$\left\{\begin{array}{l}{{x}^{2},-1≤x<0}\\{kx-1,0≤x≤1}\end{array}\right.$,
∴(-1)2=k×1-1,解得k=2,
∴f($\frac{17}{4}$)=f(2×2+$\frac{1}{4}$)=f($\frac{1}{4}$)=$\frac{1}{4}$k-1=-$\frac{1}{2}$
故选:B
点评 本题考查函数的周期性,涉及分段函数的解析式,求出k值是解决问题的关键,属基础题.


科目:高中数学 来源: 题型:选择题
 某大学的大门蔚为壮观,有个学生想搞清楚门洞拱顶D到其正上方A点的距离,他站在地面C处,利用皮尺量得BC=9米,利用测角仪测得仰角∠ACB=45°,测得仰角∠BCD后通过计算得到sin∠ACD=$\frac{\sqrt{26}}{26}$,则AD的距离为( )
某大学的大门蔚为壮观,有个学生想搞清楚门洞拱顶D到其正上方A点的距离,他站在地面C处,利用皮尺量得BC=9米,利用测角仪测得仰角∠ACB=45°,测得仰角∠BCD后通过计算得到sin∠ACD=$\frac{\sqrt{26}}{26}$,则AD的距离为( )| A. | 2米 | B. | 2.5米 | C. | 3米 | D. | 4米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
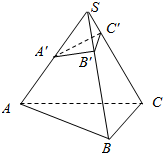 如图所示,在三棱锥S-ABC中,A′,B′,C′分别在棱SA,SB,SC上,且SA′:SA=1:2,SB′:SB=1:3,SC′:SC=1:4,求VS-ABC与VS-A′B′C′的比.
如图所示,在三棱锥S-ABC中,A′,B′,C′分别在棱SA,SB,SC上,且SA′:SA=1:2,SB′:SB=1:3,SC′:SC=1:4,求VS-ABC与VS-A′B′C′的比.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com