
【题目】已知函数 ![]() 的最小正周期为4π,则( )
的最小正周期为4π,则( )
A.函数f(x)的图象关于原点对称
B.函数f(x)的图象关于直线 ![]() 对称
对称
C.函数f(x)图象上的所有点向右平移 ![]() 个单位长度后,所得的图象关于原点对称
个单位长度后,所得的图象关于原点对称
D.函数f(x)在区间(0,π)上单调递增
科目:高中数学 来源: 题型:
【题目】A,B两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
A组:10,11,12,13,14,15,16
B组:12,13,15,16,17,14,a
假设所有病人的康复时间互相独立,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果人康复时间的方差相等?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设边a,b,c所对的角为A,B,C,且A,B,C都不是直角,(bc﹣8)cosA+accosB=a2﹣b2 . (Ⅰ)若b+c=5,求b,c的值;
(Ⅱ)若 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=eax+λlnx,其中a<0,0<λ< ![]() ,e是自然对数的底数
,e是自然对数的底数
(1)求证:函数f(x)有两个极值点;
(2)若﹣e≤a<0,求证:函数f(x)有唯一零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的最大值为2,它的最小正周期为2π. (Ⅰ)求函数f(x)的解析式;
的最大值为2,它的最小正周期为2π. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)若g(x)=cosxf(x),求g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=4,BC=2,D,E分别为边AC,AB的中点,点F,G分别为线段CD,BE的中点.将△ADE沿DE折起到△A1DE的位置,使∠A1DC=60°.点Q为线段A1B上的一点,如图2. 
(Ⅰ)求证:A1F⊥BE;
(Ⅱ)线段A1B上是否存在点Q使得FQ∥平面A1DE?若存在,求出A1Q的长,若不存在,请说明理由;
(Ⅲ)当 ![]() 时,求直线GQ与平面A1DE所成角的大小.
时,求直线GQ与平面A1DE所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式y=axb(a,b为大于0的常数).现随机抽取6件合格产品,测得数据如下:
尺寸(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量(g) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)根据所给数据,求y关于x的回归方程;
(Ⅱ)按照某项指标测定,当产品质量与尺寸的比在区间( ![]() ,
, ![]() )内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
)内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
附:对于一组数据(v1 , u1),(v2 , u2),…,(vn , un),其回归直线u=α+βv的斜率和截距的最小二乘估计分别为 ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点. 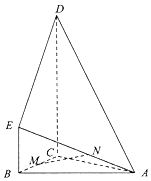
(1)若N是棱AE上的动点,求证:DE⊥MN;
(2)若平面ADE与平面ABC所成锐二面角为60°,求棱AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com