
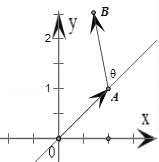
【题目】已知向量![]() ,
,![]() 是坐标原点,若
是坐标原点,若![]() ,且
,且![]() 方向是沿
方向是沿![]() 的方向绕着
的方向绕着![]() 点按逆时针方向旋转
点按逆时针方向旋转![]() 角得到的,则称
角得到的,则称![]() 经过一次
经过一次![]() 变换得到
变换得到![]() ,现有向量
,现有向量![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,
,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,…,如此下去,
,…,如此下去,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,设
,设![]() ,
,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.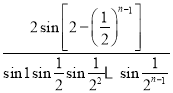 B.
B.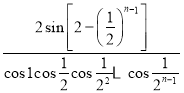
C.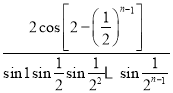 D.
D.
【答案】B
【解析】
根据题意,可得![]() ,
,![]() ,
,![]() ,即当
,即当![]() 时,一次
时,一次![]() ,
,![]() 变换将
变换将![]() 逆时针旋转1弧度,再将所得向量的长度再伸长为原来的
逆时针旋转1弧度,再将所得向量的长度再伸长为原来的![]() 倍得到向量
倍得到向量![]() .因此当
.因此当![]() 时,运用矩阵变换公式,算出
时,运用矩阵变换公式,算出![]() 逆时针旋转1弧度所得向量
逆时针旋转1弧度所得向量![]() ,从而得到
,从而得到![]() ,
,![]() ,
,![]() ,所以
,所以![]() .接下来再对
.接下来再对![]() 、
、![]() 、
、![]() 、
、![]() 各项在
各项在![]() 时的情况进行计算,对照所得结果可得只有
时的情况进行计算,对照所得结果可得只有![]() 项是正确的选项
项是正确的选项
根据题意,![]() ,
,![]()
![]() 一次
一次![]() ,
,![]() 变换就是将向量
变换就是将向量![]() 逆时针旋转1弧度,再将长度伸长为原来的
逆时针旋转1弧度,再将长度伸长为原来的![]() 倍,
倍,
即![]() 由
由![]() 逆时针旋转1弧度而得,且
逆时针旋转1弧度而得,且![]()
设向量![]() 逆时针旋转1弧度,所得的向量为
逆时针旋转1弧度,所得的向量为![]() ,则有
,则有![]() ,
,
![]()
![]() ,即向量
,即向量![]() 逆时针旋转1弧度,
逆时针旋转1弧度,
得到向量![]() ,再将
,再将![]() 的模长度伸长为原来的
的模长度伸长为原来的![]() 倍,
倍,
得到![]() ,
,![]() ,
,![]()
因此当![]() 时,
时,![]() ,
,![]() ,
,![]() ,即
,即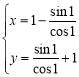 ,由此可得
,由此可得![]()
对于![]() ,当
,当![]() 时
时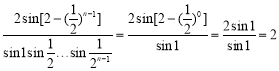 ,与计算结果不相等,故
,与计算结果不相等,故![]() 不正确;
不正确;
对于![]() ,当
,当![]() 时
时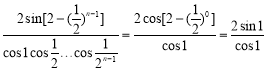 ,与计算结果相等,故
,与计算结果相等,故![]() 正确;
正确;
对于![]() ,当
,当![]() 时
时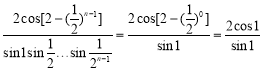 ,与计算结果不相等,故
,与计算结果不相等,故![]() 不正确;
不正确;
对于![]() ,当
,当![]() 时
时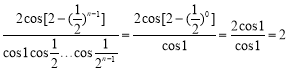 ,与计算结果不相等,故
,与计算结果不相等,故![]() 不正确
不正确
故选:B


科目:高中数学 来源: 题型:
【题目】在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
作物产量( | 400 | 500 |
概率 |
|
|
作物市场价格(元/ | 5 | 6 |
概率 |
|
|
(1)设![]() 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求![]() 的分布列(利润
的分布列(利润![]() 产量
产量![]() 市场价格
市场价格![]() 成本);
成本);
(2)若在这块地上连续3季种植此作物,求这3季中的利润都在区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),已知当x∈[0,1]时,f(x)=(![]() )1﹣x,则
)1﹣x,则
①2是函数f(x)的一个周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④x=1是函数f(x)的一个对称轴;
⑤当x∈(3,4)时,f(x)=(![]() )x﹣3.
)x﹣3.
其中所有正确命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 经过点
经过点![]() ,且与极轴所成的角为
,且与极轴所成的角为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() 和
和![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列三个命题:
变化时,给出下列三个命题:
①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②
轴对称;②![]() 的最小值为2;
的最小值为2;
③存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个,
仅有两个,
其中,所有正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD=![]() ,AP=
,AP=![]() ,PC=
,PC=![]() .
.
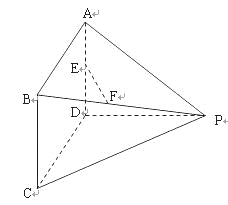
(Ⅰ)求证:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求证BE⊥DP;
(Ⅲ)若∠CDP=120°,求该多面体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1:![]() ,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
(1)求曲线C1的参数方程和C2的直角坐标方程;
(2)设M,N分别为曲线C1,C2上的动点,求|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC﹣A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
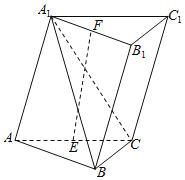
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M:![]() 1(a>b>0)的长轴长为2
1(a>b>0)的长轴长为2![]() ,离心率为
,离心率为![]() ,过点(0,1)的直线l与M交于A,B两点,且
,过点(0,1)的直线l与M交于A,B两点,且![]() .
.
(1)求M的方程;
(2)求点P的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com