[题目]用数学归纳法证明1+2+3+-+n2= .则当n=k+1时左端应在n=k的基础上加上( )A.k2+1B.(k+1)2C.D.(k2+1)+(k2+2)+(k2+3)+-+(k+1)2 题目和参考答案——青夏教育精英家教网—

【题目】用数学归纳法证明1+2+3+…+n2= ，则当n=k+1时左端应在n=k的基础上加上（）
A.k2+1
B.（k+1）2
C.
D.（k2+1）+（k2+2）+（k2+3）+…+（k+1）2

【答案】D
【解析】解：当n=k时，等式左端=1+2+…+k2 ，
当n=k+1时，等式左端=1+2+…+k2+k2+1+k2+2+…+（k+1）2 ，增加了项（k2+1）+（k2+2）+（k2+3）+…+（k+1）2 ．
故选D．
首先分析题目求用数学归纳法证明1+2+3+…+n2= 时，当n=k+1时左端应在n=k的基础上加上的式子，可以分别使得n=k，和n=k+1代入等式，然后把n=k+1时等式的左端减去n=k时等式的左端，即可得到答案．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中，直线的参数方程为，其中为参数，，再以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为，其中，，直线与曲线交于两点.

（1）求的值；

（2）已知点，且，求直线的普通方程.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ax3+bx2的图象经过点M（1，4），曲线在点M处的切线恰好与直线x+9y=0垂直．
（1）求实数a，b的值；
（2）若函数f（x）在区间[m，m+1]上单调递增，求m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】有4名男生，3名女生排成一排：
（1）从中选出3人排成一排，有多少种排法？
（2）若男生甲不站排头，女生乙不站在排尾，则有多少种不同的排法？
（3）要求女生必须站在一起，则有多少种不同的排法？
（4）若3名女生互不相邻，则有多少种不同的排法？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=|x|+ ﹣1（x≠0）
（1）当m=1时，判断f（x）在（﹣∞，0）的单调性，并用定义证明；
（2）若对任意x∈（1，+∞），不等式 f（log2x）＞0恒成立，求m的取值范围．
（3）讨论f（x）零点的个数．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】自然数按如图的规律排列：则上起第2007行左起2008列的数为（）

A.20072
B.20082
C.2006×2007
D.2007×2008

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知定义在（﹣1，1）上的奇函数是增函数，且．
（1）求函数f（x）的解析式；
（2）解不等式f（t﹣1）+f（2t）＜0．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，将自然数按如下规则“放置”在平面直角坐标系中，使其满足条件：①每个自然数“放置”在一个“整点”（横纵坐标均为整数的点）上；②0在原点，1在（0，1）点，2在（1，1）点，3在（1，0）点，4在（1，﹣1）点，5在（0，﹣1）点，…，即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上，则放置数字（2n+1）2 ， n∈N*的整点坐标是．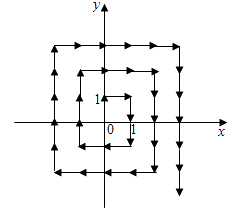

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知定义域为（0，+∞）的函数f（x）满足：（1）对任意x∈（0，+∞），恒有f（2x）=2f（x）成立；（2）当x∈（1，2]时，f（x）=2﹣x．给出如下结论：
①对任意m∈Z，有f（2m）=0；
②函数f（x）的值域为[0，+∞）；
③存在n∈Z，使得f（2n+1）=9；
正确的有（）
A.①②③
B.①②
C.①③
D.②③

查看答案和解析>>

同步练习册答案