
科目:高中数学 来源:2017届贵州遵义市高三上期中数学(文)试卷(解析版) 题型:解答题
已知函数 ,其中
,其中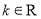 且
且 .
.
(1)求函数 的单调区间;
的单调区间;
(2)当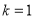 时,若存在
时,若存在 ,使
,使 成立,求实数
成立,求实数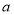 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届贵州遵义市高三上期中数学(理)试卷(解析版) 题型:选择题
某校高三年级有1000名学生,随机编号为0001,0002,...,1000,现按系统抽样方法,从中抽出200人,若0122号被抽到了,则下列编号也被抽到的是( )
A. 0927 B. 0834 C. 0726 D. 0116
查看答案和解析>>
科目:高中数学 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
某公司对新招聘的员工张某进行综合能力测试,共设置了 三个测试项目,假定张某通过项目
三个测试项目,假定张某通过项目 的概率为
的概率为 ,通过项目
,通过项目 的概率均为
的概率均为 ,且这三个测试项目能否通过相互独立.
,且这三个测试项目能否通过相互独立.
(1)用随机变量 表示张某在测试中通过的项目个数,求
表示张某在测试中通过的项目个数,求 的概率分布和数学期望
的概率分布和数学期望 (用
(用 表示);
表示);
(2)若张某通过一个项目的概率最大,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
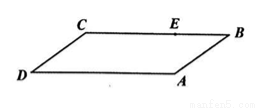
如图,有一块平行四边形绿地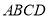 ,经测量
,经测量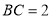 百米,
百米, 百米,
百米,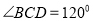 ,拟过线段
,拟过线段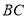 上一点
上一点 设计一条直路
设计一条直路 (点
(点 在四边形
在四边形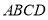 的边上,不计路的宽度),
的边上,不计路的宽度), 将绿地分成两部分,且右边面积是左边面积的3倍,设
将绿地分成两部分,且右边面积是左边面积的3倍,设 百米,
百米,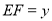 百米.
百米.
(1)当点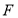 与点
与点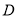 重合时,试确定点
重合时,试确定点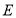 的位置;
的位置;
(2)试求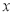 的值,使路
的值,使路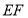 的长度
的长度 最短.
最短.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二文上周检五数学试卷(解析版) 题型:解答题
已知数列 中,
中,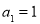 , 且
, 且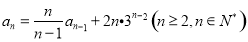 .
.
(1)求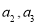 的值及数列
的值及数列 的通项公式;
的通项公式;
(2)令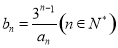 , 数列
, 数列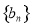 的前
的前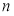 项和为
项和为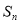 , 试比较
, 试比较 与
与 的大小;
的大小;
(3)令 , 数列
, 数列 的前
的前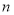 项和为
项和为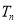 , 求证: 对任意
, 求证: 对任意 , 都有
, 都有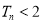 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com