
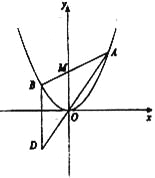
【题目】如图所示,已知抛物线![]() ,过点
,过点![]() 任作一直线与
任作一直线与![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() 为坐标原点).
为坐标原点).
(1)证明: 动点![]() 在定直线上;
在定直线上;
(2)作![]() 的任意一条切线
的任意一条切线![]() (不含
(不含![]() 轴), 与直线
轴), 与直线![]() 相交于点
相交于点![]() 与(1)中的定直线相交于点
与(1)中的定直线相交于点![]() .
.
证明: ![]() 为定值, 并求此定值.
为定值, 并求此定值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】给出下列结论:
动点![]() 分别到两定点(-3,0)、(3,0) 连线的斜率之乘积为
分别到两定点(-3,0)、(3,0) 连线的斜率之乘积为![]() ,设
,设![]() 的轨迹为曲线
的轨迹为曲线![]() ,分别为曲线
,分别为曲线![]() 的左、右焦点,则下列说法中:
的左、右焦点,则下列说法中:
(1)曲线![]() 的焦点坐标为
的焦点坐标为![]() ;
;
(2)当![]() 时,
时,![]() 的内切圆圆心在直线
的内切圆圆心在直线![]() 上;
上;
(3)若![]() ,则
,则![]() ;
;
(4)设![]() ,则
,则![]() 的最小值为
的最小值为![]() ;
;
其中正确的序号是:_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定矩形春季校园足球联赛,为迎接此次联赛,甲同学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录如下表:
身高( | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
人数 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
(1)请计算这20名学生的身高中位数、众数,并补充完成下面的茎叶图;

(2)身高为185![]() 和188
和188![]() 的四名学生分别为
的四名学生分别为![]() ,
,![]() ,
,![]() ,
,![]() ,先从这四名学生中选2名担任正副门将,请利用列举法列出所有可能情况,并求学生
,先从这四名学生中选2名担任正副门将,请利用列举法列出所有可能情况,并求学生![]() 入选正门将的概率.
入选正门将的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() .
.
(Ⅰ)求满足![]() 的概率;
的概率;
(Ⅱ)设三条线段的长分别为![]() 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com