
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
(1)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.
科目:高中数学 来源: 题型:
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数![]() 为
为![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
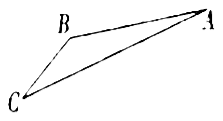
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,当
,当![]()
![]() ,
,![]() 时,有
时,有![]() 成立.
成立.
(Ⅰ)判断![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅱ)若![]() 对所有的
对所有的![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如图5所示:将
的一段图象如图5所示:将![]() 的图像向右平移
的图像向右平移![]() 个单位,可得到函数
个单位,可得到函数![]() 的图象,且图像关于原点对称,
的图象,且图像关于原点对称,

(1)求![]() 的值;
的值;
(2)求![]() 的最小值,并写出
的最小值,并写出![]() 的表达式;
的表达式;
(3)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上最小值为
上最小值为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:指数函数y=(1-a)x是R上的增函数,命题q:不等式ax2+2x-1>0有解.若命题p是真命题,命题q是假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() .
.
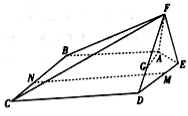
(1)已知点![]() 在线段
在线段![]() 上,确定
上,确定![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,
向上翻折,![]() 与
与![]() 恰好重合,求三棱锥
恰好重合,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com