
分析 (Ⅰ)利用向量模的计算方法,求出D的轨迹方程,即可求出动点D的轨迹.
(Ⅱ)|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|=$\sqrt{(x-1)^{2}+(y+\sqrt{3})^{2}}$,问题转化为圆(x-3)2+y2=1上的点与点P(1,-$\sqrt{3}$)间距离的最大值.
解答 解:(1)设D(x,y),由$\overrightarrow{CD}$=(x-3,y)及|$\overrightarrow{CD}$|=1
知(x-3)2+y2=1,(4分)
即动点D的轨迹为以点C为圆心的单位圆. (6分)
(2)$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$=(-1,0)+(0,$\sqrt{3}$)+(x,y)=(x-1,y+$\sqrt{3}$),
∴|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|=$\sqrt{(x-1)^{2}+(y+\sqrt{3})^{2}}$.(8分)
问题转化为圆(x-3)2+y2=1上的点与点P(1,-$\sqrt{3}$)间距离的最大值.
∵圆心C(3,0)与点P(1,-$\sqrt{3}$)之间的距离为$\sqrt{(3-1)^{2}+(0+\sqrt{3})^{2}}$=$\sqrt{7}$,(10分)
故|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|的最大值为$\sqrt{7}$+1.(12分)
点评 本题考查轨迹方程,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0,0) | B. | (2,2,0) | C. | (1,1,0) | D. | (0,1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 2 $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
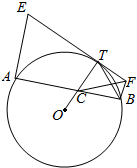 已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:
已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,$\frac{3}{2}$) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com