
【题目】如图,真四棱柱![]() 的底面是菱形,
的底面是菱形,![]() ,
,![]() ,
,![]() ,E,M,N分别是BC,
,E,M,N分别是BC,![]() ,
,![]() 的中点.
的中点.
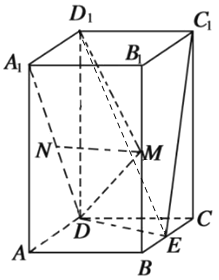
(1)证明:![]() 面
面![]() ;
;
(2)求平面DMN与平面![]() 所成锐角的正切值.
所成锐角的正切值.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)由余弦定理可得![]() ,进而可得
,进而可得![]() ,由正棱柱的几何特征可得
,由正棱柱的几何特征可得![]() ,由线面垂直的判定即可得解;
,由线面垂直的判定即可得解;
(2)连接ME,由题意可得四边形DNME为平行四边形,DE即为平面DMN与平面![]() 的交线,由线面垂直的判定可得
的交线,由线面垂直的判定可得![]() 面
面![]() ,进而可得
,进而可得![]() 即为平面DMN与平面
即为平面DMN与平面![]() 所成的平面角,即可得解.
所成的平面角,即可得解.
(1)证明:∵在菱形ABCD中,![]() ,
,![]() ,且E为BC中点,
,且E为BC中点,
∴![]() ,∴
,∴![]() 即
即![]() ,
,
又棱柱![]() 是直四棱柱,∴
是直四棱柱,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 面
面![]() ;
;
(2)连接ME,

∵E,M,N分别是BC,![]() ,
,![]() 的中点,
的中点,
∴![]() 且
且![]() ,
,
∴![]() 且
且![]() ,∴四边形DNME为平行四边形,
,∴四边形DNME为平行四边形,
从而可知:DE即为面DMN与面![]() 的交线,
的交线,
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() 面
面![]() ,
,
∴![]() 且
且![]() ,
,
则![]() 即为平面DMN与平面
即为平面DMN与平面![]() 所成的平面角,
所成的平面角,
在![]() 中,
中,![]() ,
,
故平面DMN与平面![]() 所成锐角的正切值为
所成锐角的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】椭圆![]() 的焦距是
的焦距是![]() ,长轴长是短轴长3倍,任作斜率为
,长轴长是短轴长3倍,任作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(如图所示),且点
两点(如图所示),且点![]() 在直线
在直线![]() 的左上方.
的左上方.

(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)证明:![]() 的内切圆的圆心在一条定直线上。
的内切圆的圆心在一条定直线上。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是![]() (t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
(t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“网购”已经成为我们日常生活中的一部分,某地区随机调查了100名男性和100名女性在“双十一”活动中用于网购的消费金额,数据整理如下:
男性消费金额频数分布表
消费金额 (单位:元) | 0~500 | 500~1000 | 1000~1500 | 1500~2000 | 2000~3000 |
人数 | 15 | 15 | 20 | 30 | 20 |
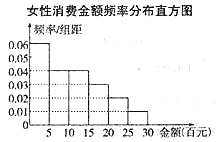
(1)试分别计算男性、女性在此活动中的平均消费金额;
(2)如果分别把男性、女性消费金额与中位数相差不超过200元的消费称作理性消费,试问是否有5成以上的把握认为理性消费与性别有关.
附: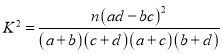
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年春节期间全国流行在微信群里发、抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如表:

(I)求产生的手气红包的金额不小于9元的频率;
(Ⅱ)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)在这50个红包组成的样本中,将频率视为概率.
(i)若红包金额在区间[21,25]内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
(ii)随机抽取手气红包金额在[1,5)∪[﹣21,25]内的两名幸运者,设其手气金额分别为m,n,求事件“|m﹣n|>16”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区组织“学习强国”的知识竞赛,从参加竞赛的市民中抽出40人,将其成绩分成以下6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第2,3,4组中按分层抽样抽取8人,则第2,3,4组抽取的人数依次为( )
,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第2,3,4组中按分层抽样抽取8人,则第2,3,4组抽取的人数依次为( )
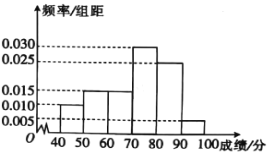
A.1,3,4B.2,3,3C.2,2,4D.1,1,6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,ACBC,D,E分别是A1B1,BC的中点.求证:

(1)平面ACD⊥平面BCC1B1;
(2)B1E∥平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线C1的参数方程为![]() (t为参数,0<α<π),曲线C2的参数方程为
(t为参数,0<α<π),曲线C2的参数方程为 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C2的极坐标方程;
(2)设曲线C1与曲线C2的交点分别为A,B,M(﹣2,0),求|MA|2+|MB|2的最大值及此时直线C1的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com