
分析 ①当θ=$\frac{π}{4}$时,S中直线的斜率为k=-$\frac{b}{a}$;②(0,0)不满足方程$\frac{sinθ}{a}$x+$\frac{cosθ}{b}$y=1,S中的所有直线不可能覆盖整个平面;③当a=b时,方程变为xsinθ+ycosθ=a,存在定点(0,0),该定点到S中的所有直线的距离均相等.
解答 解:①当θ=$\frac{π}{4}$时,直线方程变为$\frac{\sqrt{2}x}{2a}+\frac{\sqrt{2}y}{2b}=1$
S中直线的斜率为k=-$\frac{b}{a}$,故①错误;
②∵(0,0)不满足方程$\frac{sinθ}{a}$x+$\frac{cosθ}{b}$y=1,∴S中的所有直线不可覆盖整个平面,故②错误;
③当a=b时,方程为xsinθ+ycosθ=a,存在定点(0,0),该定点到S中的所有直线的距离均相等,故③正确.
故答案为:③.
点评 本题考查命题的真假判断与应用,考查直线系方程的应用,要明确直线系中直线的性质,结合三角函数的性质,判断各个命题的正确性,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x0∈N,x02+2x0≤3 | B. | ?x∈N,x2+2x≤3 | C. | ?x0∈N,x02+2x0<3 | D. | ?x∈N,x2+2x<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=4x2-6 | B. | f(x)=$\frac{1}{4}{x}^{2}-\frac{3}{2}x-\frac{15}{4}$ | ||
| C. | f(x)=$\frac{1}{4}{x}^{2}+\frac{3}{2}x-\frac{15}{4}$ | D. | f(x)=x2-2x-5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
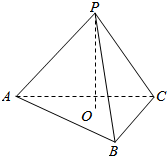 如图,三棱锥P-ABC的三条侧棱两两垂直,即:PA⊥PB、PB⊥PC、PC⊥PA,且PO⊥平面ABC并交平面ABC于点O,请问点O是△ABC的什么心(内心、外心、垂心、重心、中心等)?并证明你的结论.
如图,三棱锥P-ABC的三条侧棱两两垂直,即:PA⊥PB、PB⊥PC、PC⊥PA,且PO⊥平面ABC并交平面ABC于点O,请问点O是△ABC的什么心(内心、外心、垂心、重心、中心等)?并证明你的结论.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com