
【题目】已知等差数列{an}中,a5=8,a10=23.
(1)令![]() ,证明:数列{bn}是等比数列;
,证明:数列{bn}是等比数列;
(2)求数列{nbn}的前n项和Sn.
【答案】(1)见解析(2)Sn=(n﹣1)2n+1+2.
【解析】
(1)由题意可得an=3n-7,则![]() ,即可得证;
,即可得证;
(2)由nbn=n2n利用错位相减法即可求得Sn,即可得解.
(1)证明:设等差数列{an}的公差为d,∵a5=8,a10=23,
∴a1+4d=8,a1+9d=23,
联立解得:a1=-4,d=3,
∴an=-4+3(n﹣1)=3n-7.
∴![]() ,
,
∴![]() 2.
2.
∴数列{bn}是等比数列,首项为2,公比为2.
(2)nbn=n2n.
∴数列{nbn}的前n项和Sn=2+2×22+3×23+……+n2n.
∴2Sn=22+2×23+……+(n﹣1)2n+n2n+1.
∴两式相减得﹣Sn=2+22+……+2n﹣n2n+1![]() n2n+1.
n2n+1.
∴Sn=(n﹣1)2n+1+2.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.
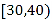
(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,椭圆
轴的正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程(写成一般式)和椭圆
的普通方程(写成一般式)和椭圆![]() 的直角坐标方程(写成标准方程);
的直角坐标方程(写成标准方程);
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为角A,B,C的对边,且满足cosC+sinC![]() .
.
(1)求角B的大小;
(2)若a+c的最大值为10,求边长b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率作了调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如表:
个人所得税税率表 | 个人所得税税率表 | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率 | 级数 | 全月应纳税所得额 | 税率 |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
|
|
|
|
|
|
(1)假如小明某月的工资、薪金等税前收入为7500元,请你帮小明算一下调整后小明的实际收入比调整前增加了多少?
(2)某税务部门在小明所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入 |
|
|
|
|
|
|
人数 | 40 | 30 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量X表示抽到作为宣讲员的收入在
的人群中按分层抽样抽取7人,再从中选3人作为新纳税法知识宣讲员,用随机变量X表示抽到作为宣讲员的收入在![]() 元的人数,求X的分布列与数学期望.
元的人数,求X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com