
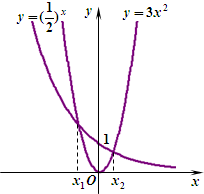
 如图,是函数
如图,是函数 和y=3x2图象的一部分,其中x=x1,x2(-1<x1<0<x2)时,两函数值相等.
和y=3x2图象的一部分,其中x=x1,x2(-1<x1<0<x2)时,两函数值相等.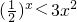 ;②当x>x2时,
;②当x>x2时,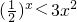 ,试判定命题①②的真假并说明理由;
,试判定命题①②的真假并说明理由; ,3×(-10)2=300,
,3×(-10)2=300,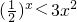 不成立;
不成立; 在[x2,+∞)上是减函数,函数y=3x2在[x2,+∞)上是增函数,
在[x2,+∞)上是减函数,函数y=3x2在[x2,+∞)上是增函数,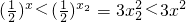 ;
; ,则f(0)=-1<0,
,则f(0)=-1<0,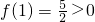 ,
, 在区间(0,+∞)上单调递增,
在区间(0,+∞)上单调递增, 在[x2,+∞)上是减函数,函数y=3x2在[x2,+∞)上是增函数,即可证得;
在[x2,+∞)上是减函数,函数y=3x2在[x2,+∞)上是增函数,即可证得; ,的零点问题,再利用零点存在性定理,判断零点范围即可作出证明.
,的零点问题,再利用零点存在性定理,判断零点范围即可作出证明.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
 如图:是y=f(x)=
如图:是y=f(x)=| a | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
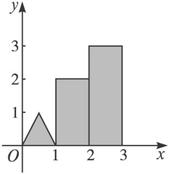
 某商品在近30天内每件的销售价格P元和时间t(t∈N)的关系如图所示.
某商品在近30天内每件的销售价格P元和时间t(t∈N)的关系如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
如图:是y=f(x)=![]() x3﹣2x2+3a2x的导函数y=f'(x)的简图,它与x轴的交点是(1,0)和(3,0)
x3﹣2x2+3a2x的导函数y=f'(x)的简图,它与x轴的交点是(1,0)和(3,0)
(1)求y=f(x)的极小值点和单调减区间
(2)求实数a的值.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省巢湖市无为县开城中学高二(下)期中数学试卷(文科)(解析版) 题型:解答题
 x3-2x2+3a2x的导函数y=f'(x)的简图,它与x轴的交点是(1,0)和(3,0)
x3-2x2+3a2x的导函数y=f'(x)的简图,它与x轴的交点是(1,0)和(3,0)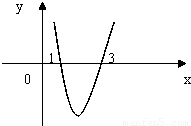
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com