
【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
科目:高中数学 来源: 题型:
【题目】为选拔参加“全市高中数学竞赛”的选手,某中学举行了一次“数学竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
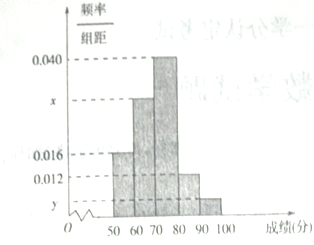
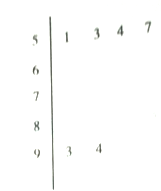
(1)求样本容![]() 和频率分布直方图中
和频率分布直方图中![]() 的值并求出抽取学生的平均分;
的值并求出抽取学生的平均分;
(2)在选取的样本中,从竞赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生参加“全市中数学竞赛”求所抽取的
名学生参加“全市中数学竞赛”求所抽取的![]() 名学生中至少有一人得分在
名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
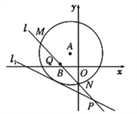
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过
的年平均浓度不得超过![]() 微克/立方米,
微克/立方米,![]() 的24小时平均浓度不得超过
的24小时平均浓度不得超过![]() 微克/立方米.某城市环保部门随机抽取了一居民区去年20天
微克/立方米.某城市环保部门随机抽取了一居民区去年20天![]() 的24小时平均浓度的监测数据,数据统计如下:
的24小时平均浓度的监测数据,数据统计如下:
组别 |
(微克/立方米) | 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
(1)从样本中![]() 的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天
的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天
![]() 的24小时平均浓度超过75微克/立方米的概率;
的24小时平均浓度超过75微克/立方米的概率;
(2)求样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境是
的年平均浓度考虑,判断该居民区的环境是
否需要改进?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(A)已知数列![]() 满足
满足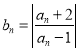 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)由(1)写出数列![]() 的前
的前![]() 项和
项和![]() ,并用数学归纳法证明.
,并用数学归纳法证明.
(B)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() .
.
(1)猜想![]() 的表达式,并用数学归纳法证明;
的表达式,并用数学归纳法证明;
(2)设![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com