
【题目】已知公比不为1的等比数列{an}的前5项积为243,且2a3为3a2和a4的等差中项.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=bn﹣1log3an+2(n≥2且n∈N*),且b1=1,求数列 ![]() 的前n项和Sn .
的前n项和Sn .
【答案】
(1)解:由前5项积为243,即为a1a2a3a4a5=243,
即有a1a5=a2a4=a32,即a35=243,
得:a3=3,设等比数列的公比为q,
由2a3为3a2和a4的等差中项得:4a3=3a2+a4,
即 ![]() ,
,
由公比不为1,解得:q=3,
所以an=a3qn﹣3,
即 ![]()
(2)解:由bn=bn﹣1log3an+2=bn﹣1n,
得 ![]() ,
,
数列 ![]() ,
,
所以它的前n项和 ![]() .
.
【解析】(1)运用等比数列的性质可得a3=3,设等比数列的公比为q,运用等差数列中项的性质,结合等比数列通项公式,解得q=3,即可得到所求数列{an}的通项公式;(2)求得bn=bn﹣1log3an+2=bn﹣1n,运用数列恒等式bn=b1 ![]() …
… ![]() =n!,求出
=n!,求出 ![]() ,运用裂项相消求和即可得到所求和.
,运用裂项相消求和即可得到所求和.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(Ⅱ)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
(1函数f(x)=loga(2x﹣1)﹣1的图象过定点(1,0);
(2化简2 ![]() +lg5lg2+(lg2)2﹣lg2的结果为25;
+lg5lg2+(lg2)2﹣lg2的结果为25;
(3若loga ![]() <1,则a的取值范围是(1,+∞);
<1,则a的取值范围是(1,+∞);
(4若2﹣x﹣2y>lnx﹣ln(﹣y)(x>0,y<0),则x+y<0.
其中所有正确命题的序号是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,g(x)= ![]() (a∈R,e为自然对数的底数)
(a∈R,e为自然对数的底数)
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在![]() 上无零点,求a的最小值;
上无零点,求a的最小值;
(Ⅲ)若对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+θ)( A>0,ω>0,|θ|< ![]() )的最小正周期为π,且图象上有一个最低点为M(
)的最小正周期为π,且图象上有一个最低点为M( ![]() ,﹣3).
,﹣3).
(1)求f(x)的解析式;
(2)求函数f(x)在[0,π]的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示. 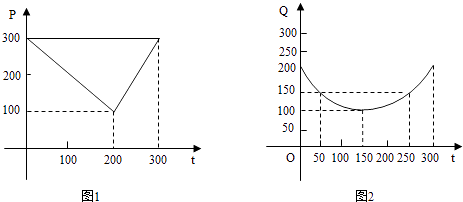
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中正确的有
①函数y= ![]() 的定义域是{x|x≠0};
的定义域是{x|x≠0};
②lg ![]() =lg(x﹣2)的解集为{3};
=lg(x﹣2)的解集为{3};
②31﹣x﹣2=0的解集为{x|x=1﹣log32};
④lg(x﹣1)<1的解集是{x|x<11}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com