
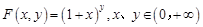 .
.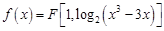 与直线
与直线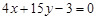 垂直的切线方程;
垂直的切线方程;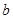 使曲线
使曲线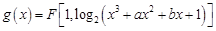 在
在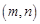 点处的切线斜率为
点处的切线斜率为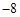 ,且
,且 ,求实数
,求实数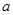 的取值范围.
的取值范围.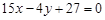 . (2)
. (2)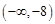 。
。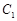 的切线与直线
的切线与直线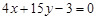 垂直,故令
垂直,故令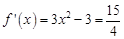 得
得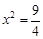 得到
得到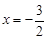 ,进而得到切线方程。
,进而得到切线方程。
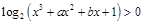 ,得
,得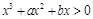
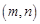 ,故有
,故有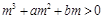 ,构造函数利用导数求解不等式转化为
,构造函数利用导数求解不等式转化为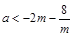 在
在 上有解来解决。
上有解来解决。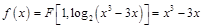 ,
, 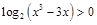 ①, -------------------------2分
①, -------------------------2分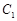 的切线与直线
的切线与直线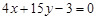 垂直,故令
垂直,故令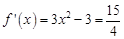 得
得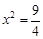 ②,由①②知应取
②,由①②知应取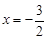 ,得
,得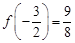 ,切点为
,切点为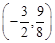 ,
,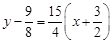 ,即
,即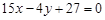 .------------------4分
.------------------4分
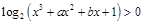 ,得
,得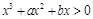
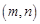 ,故有
,故有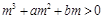 -----------------6分
-----------------6分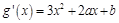 ,依题意有
,依题意有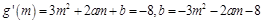
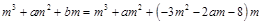
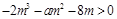 ---------------------8分
---------------------8分 上有解,即
上有解,即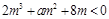 在
在 上有解,
上有解, 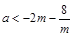 在
在 上有解,-------- -------------10分
上有解,-------- -------------10分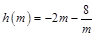 ,则
,则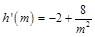 ,在
,在 上恒有
上恒有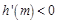
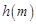 是
是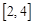 上的减函数,
上的减函数,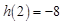 ,所以实数
,所以实数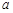 的取值范围是
的取值范围是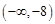 --------------12分
--------------12分

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源:不详 题型:解答题
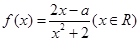
 时,求曲线
时,求曲线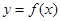 在点
在点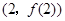 处的切线方程;
处的切线方程;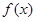 在区间
在区间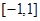 上是增函数,求实数
上是增函数,求实数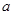 的取值范围
的取值范围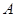 ;
;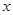 的方程
的方程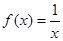 的两个根为
的两个根为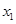 、
、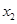 ,若对任意
,若对任意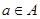 ,
,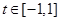 ,不等式
,不等式 恒成立,求
恒成立,求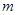 的取值范围.
的取值范围. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
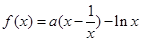
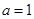 时,求曲线
时,求曲线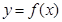 在点
在点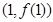 处的切线方程;
处的切线方程;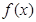 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数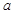 的取值范围;
的取值范围;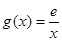 ,若在
,若在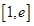 上至少存在一点
上至少存在一点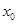 使
使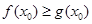 成立,求实数
成立,求实数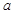 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com