
【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
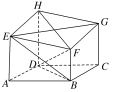
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
【答案】见解析
【解析】解:(1)证明:连接AC,由AE ![]() CG可知四边形AEGC为平行四边形.
CG可知四边形AEGC为平行四边形.
所以EG∥AC,而AC⊥BD,AC⊥BF,所以EG⊥BD,EG⊥BF,
因为BD∩BF=B,所以EG⊥平面BDHF,又DF平面BDHF,所以EG⊥DF。
(2)设AC∩BD=O,EG∩HF=P,由已知可得:平面ADHE∥平面BCGF,所以EH∥FG,同理可得:EF∥HG,所以四边形EFGH为平行四边形,所以P为EG的中点,O为AC的中点,所以OP綊AE,
从而OP⊥平面ABCD,
又OA⊥OB,所以OA,OB,OP两两垂直,由平面几何知识,得BF=2。
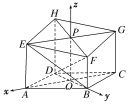
如图,建立空间直角坐标系Oxyz,则B(0,2,0),E(2![]() ,0,3),F(0,2,2),P(0,0,3),
,0,3),F(0,2,2),P(0,0,3),
所以![]() =(2
=(2![]() ,-2,3),
,-2,3),![]() =(2
=(2![]() ,0,0,),
,0,0,),![]() =(0,2,-1).
=(0,2,-1).
设平面EFGH的法向量为n=(x,y,z),
![]()
可得![]()
令y=1,则z=2。
所以n=(0,1,2).
设BE与平面EFGH所成角为θ,则sin θ=![]() =
=![]() 。
。


科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.

(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀,请填写下面的![]() 列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| span>2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() (
(![]() ,
,![]() )的动直线
)的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
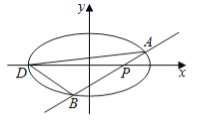
⑴求椭圆![]() 的方程:
的方程:
⑵已知![]() 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线![]() 使得
使得![]() 的面积为
的面积为![]() ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
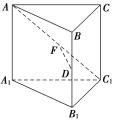
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
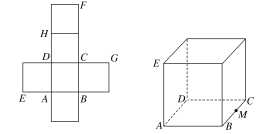
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市的高一学生中随机抽取400名同学的体重进行统计,得到如图所示频率分布直方图.
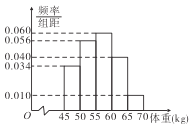
(Ⅰ)估计从该市高一学生中随机抽取一人,体重超过![]() 的概率;
的概率;
(Ⅱ)假设该市高一学生的体重![]() 服从正态分布
服从正态分布![]() .
.
(ⅰ)利用(Ⅰ)的结论估计该高一某个学生体重介于![]() 之间的概率;
之间的概率;
(ⅱ)从该市高一学生中随机抽取3人,记体重介于![]() 之间的人数为
之间的人数为![]() ,利用(ⅰ)的结论,求
,利用(ⅰ)的结论,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com