
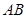 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.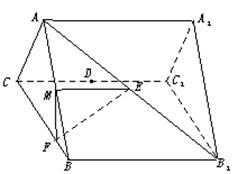
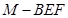 的体积.
的体积.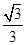 .
.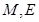 都是相应线段上的中点,因此显然有
都是相应线段上的中点,因此显然有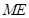 ∥
∥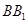 .(2)三棱锥的体积公式是
.(2)三棱锥的体积公式是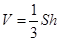 ,由于三梭锥的四个面都是三角形,故我们可以恰当地选取底面,以使得高易求(即熟知的换底法),本题中三梭锥
,由于三梭锥的四个面都是三角形,故我们可以恰当地选取底面,以使得高易求(即熟知的换底法),本题中三梭锥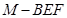 ,我们就可以以
,我们就可以以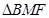 为底,而这时高就是
为底,而这时高就是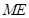 ,而高
,而高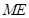 的垂直的证明可由正三梭锥的定义证得.
的垂直的证明可由正三梭锥的定义证得.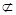 平面EFM,∴BB1∥平面EFM. 6分
平面EFM,∴BB1∥平面EFM. 6分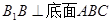 ,由(1)
,由(1)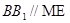 ,所以
,所以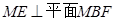 , 8分
, 8分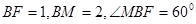 ,所以
,所以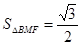 ,10分
,10分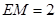 ,因此
,因此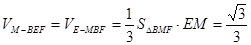 . 12分
. 12分

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com