
【题目】设集合M={x||x|<1},N={y|y=2x , x∈M},则集合R(M∩N)等于( )
A.(﹣∞, ![]() ]
]
B.( ![]() ,1)
,1)
C.(﹣∞, ![]() ]∪[1,+∞)
]∪[1,+∞)
D.[1,+∞)
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】如图是一座桥的截面图,桥的路面由三段曲线构成,曲线AB和曲线DE分别是顶点在路面A、E的抛物线的一部分,曲线BCD是圆弧,已知它们在接点B、D处的切线相同,若桥的最高点C到水平面的距离H=6米,圆弧的弓高h=1米,圆弧所对的弦长BD=10米. 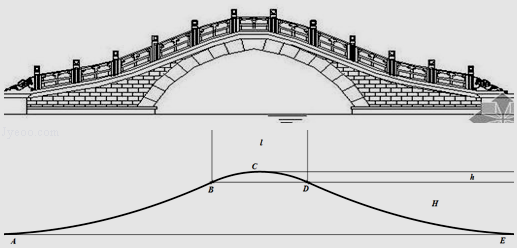
(1)求弧 ![]() 所在圆的半径;
所在圆的半径;
(2)求桥底AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]()
![]() 经过点
经过点 ![]() ,其离心率
,其离心率 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设动直线 ![]() 与椭圆
与椭圆 ![]() 相切,切点为
相切,切点为 ![]() ,且
,且 ![]() 与直线
与直线 ![]() 相交于点
相交于点 ![]() .
.
试问:在 ![]() 轴上是否存在一定点,使得以
轴上是否存在一定点,使得以 ![]() 为直径的圆恒过该定点?若存在,
为直径的圆恒过该定点?若存在,
求出该点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
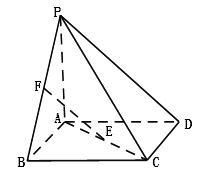
【题目】如图,四棱锥 ![]() 的底面
的底面 ![]() 为正方形,
为正方形, ![]() ⊥底面
⊥底面 ![]() ,
, ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() .
.
(Ⅰ)求证 ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角;
所成的角;
(Ⅲ)求四棱锥 ![]() 的外接球的体积.
的外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() 、
、 ![]() ,短轴两个端点为
,短轴两个端点为 ![]() 、
、 ![]() ,且四边形
,且四边形 ![]() 是边长为2的正方形.
是边长为2的正方形.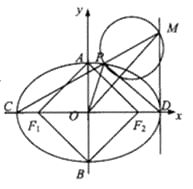
(1)求椭圆的方程;
(2)若 ![]() 、
、 ![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 ![]() 满足
满足 ![]() ,连接
,连接 ![]() ,交椭圆于点
,交椭圆于点 ![]() .证明:
.证明: ![]() 为定值.
为定值.
(3)在(2)的条件下,试问 ![]() 轴上是否存异于点
轴上是否存异于点 ![]() 的定点
的定点 ![]() ,使得以
,使得以 ![]() 为直径的圆恒过直线
为直径的圆恒过直线 ![]() 、
、 ![]() 的交点,若存在,求出点
的交点,若存在,求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣alnx+x(a∈R)
(Ⅰ)当a=1时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(Ⅱ)讨论函数y=f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=2,b1=4,且 2bn=an+an+1 , an+12=bnbn+1 .
(Ⅰ)求 a 2 , a3 , a4 及b2 , b3 , b4;
(Ⅱ)猜想{an},{bn} 的通项公式,并证明你的结论;
(Ⅲ)证明:对所有的 n∈N* , ![]()
![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com