
【题目】已知二次函数f(x)=x2+bx+c,当x∈R时f(x)=f(2﹣x)恒成立,且3是f(x)的一个零点. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=f(ax)(a>1),若函数g(x)在区间[﹣1,1]上的最大值等于5,求实数a的值.
【答案】解:(Ⅰ)由x∈R时f(x)=f(2﹣x)恒成立得函数的图像关于直线x=1对称;, ∴ ![]() =1.解得:b=﹣2
=1.解得:b=﹣2
又v的一个零点,
∴9﹣6+c=0.解得:c=﹣3.
∴f(x)=x2﹣2x﹣3
(Ⅱ)设t=ax , (a>1),
∵x∈[﹣1,1],
∴t∈[ ![]() ,a]
,a]
若f(a)=5,则由a2﹣2a﹣3=5得a=4,或a=﹣2(舍去),此时f(a)>f( ![]() ),符合题意;
),符合题意;
若f( ![]() )=5,则可得a=
)=5,则可得a= ![]() (舍去),或a=﹣
(舍去),或a=﹣ ![]() (舍去),
(舍去),
∴a=4
【解析】(I)由已知可f(x)=f(2﹣x)恒成立,且3是f(x)的一个零点,求出b,c的值,可得函数f(x)的解析式;(Ⅱ)设t=ax(a>1),由x∈[﹣1,1],可得:t∈[ ![]() ,a],结合函数g(x)在区间[﹣1,1]上的最大值等于5,分类讨论,可得满足条件的a值.
,a],结合函数g(x)在区间[﹣1,1]上的最大值等于5,分类讨论,可得满足条件的a值.
【考点精析】通过灵活运用函数的最值及其几何意义和二次函数的性质,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣a是奇函数
﹣a是奇函数
(1)求实数a的值;
(2)判断函数在R上的单调性并用函数单调性的定义证明;
(3)对任意的实数x,不等式f(x)<m﹣1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
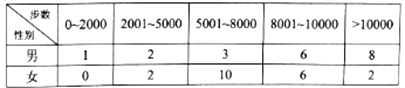
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
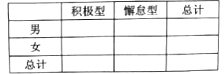
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
 附:
附: 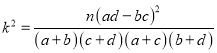 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的偶函数f(x)在[0,+∞)内是增函数,且f(3)=0,则关于x的不等式xf(x)≤0的解集为( )
A.{x|﹣3≤x≤0或x≥3}
B.{x|x≤﹣3或﹣3≤x≤0}
C.{x|﹣3≤x≤3}
D.{x|x≤﹣3或x≥3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 的极坐标方程为
的极坐标方程为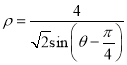 .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为曲线
为曲线![]() 上任意一点,
上任意一点, ![]() 为直线
为直线![]() 任意一点,求
任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
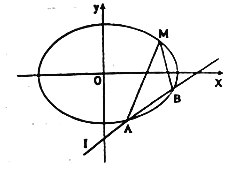
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() :
: ![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两不同的点.
两不同的点.
(1)求椭圆的方程;
(2)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() ,
, ![]() 与
与![]() 轴围成等腰三角形.
轴围成等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com