练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】把2支相同的晨光签字笔,3支相同英雄钢笔全部分给4名优秀学生,每名学生至少1支,则不同的分法有（ ）

    A. 24种 B. 28种 C. 32种 D. 36种

    【答案】B

    【解析】第一类，有一个人分到一支钢笔和一支签字笔，这中情况下的分法有：先将一支钢笔和一支签字笔分到一个人手上，有种分法，将剩余的支钢笔， 支签字笔分给剩余个同学，有种分法，那共有种；
    第二类，有一个人分到两支签字笔，这种情况下的分法有：先将两支签字笔分到一个人手上，有种情况，将剩余的支钢笔分给剩余个人，只有1种分法，那共有： 种；
    第三类，有一个人分到两支钢笔，这种情况的分法有：先将两支钢笔分到一个人手上，有种情况，再将剩余的两支签字笔和一支钢笔分给剩余的个人，有种分法，那共有： 种；
    综上所述：总共有种分法.

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，△ABC内接于圆柱的底面圆O，AB是圆O的直径，AB＝2，BC＝1，DC、EB是两条母线，且tan∠EAB＝.

    (1)求三棱锥C－ABE的体积；

    (2)证明：平面ACD⊥平面ADE；

    (3)在CD上是否存在一点M，使得MO∥平面ADE，证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2018届江西省南昌市高三第一轮】已知分别为三个内角的对边，且．

    （Ⅰ）求；

    （Ⅱ）若为边上的中线， ， ，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若是的极值点，试研究函数的单调性，并求的极值；

    （2）若在上恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

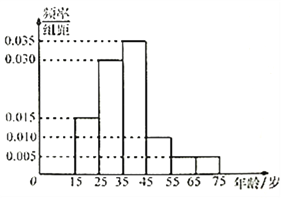
    【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: , ,,,,.把年龄落在区间和内的人分别称为“青少年”和“中老年”.

    (1)根据频率分布直方图求样本的中位数(保留两位小数)和众数

    (2)根据已知条件完成下面的2×2列联表,并判断能否有99%的把握认为关注“带一路”是否和年龄段有关?

    关注

    不关注

    合计

    青少年

    15

    中老年

    合计

    50

    50

    100

    附:参考公式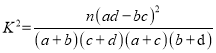，其中

    临界值表：

    /td>

    0.05

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数,

    (1)若两函数图象有两个不同的公共点,求实数的取值范围；

    (2)若, ,求实数的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中， ， ， 平面，在平行四边形中， ， ， ．

    （1）求证： 平面；

    （2）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的极坐标方程为，以极点为平面直角坐标系的原点，极轴为的正半轴，建立平面直角坐标系.

    （1）若曲线为参数）与曲线相交于两点，求；

    （2）若是曲线上的动点，且点的直角坐标为，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程是（为参数），以该直角坐标系的原点为极点， 轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）写出曲线的普通方程和直线的直角坐标方程；

    （2）设点，直线与曲线相交于两点，且，求实数的值.

    查看答案和解析>>

    同步练习册答案