
【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是![]() ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是![]() ,甲、乙两台机床加工的零件都是一等品的概率是
,甲、乙两台机床加工的零件都是一等品的概率是![]() .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率;
【答案】(1)甲、乙、丙三台机床各自加工的零件是一等品的概率分别为![]() ,
, ![]() ,
, ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)设![]() 分别表示甲、乙、丙三台机床各自加工的零件是一等品的事件,根据题意列出关于
分别表示甲、乙、丙三台机床各自加工的零件是一等品的事件,根据题意列出关于![]() 的方程组,解方程组即可得结果;(2)根据对立事件的概率为
的方程组,解方程组即可得结果;(2)根据对立事件的概率为![]() ,可得甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品的概率.
,可得甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品的概率.
试题解析:(1)设![]() 分别表示甲、乙、丙三台机床各自加工的零件是一等品的事件,那么
分别表示甲、乙、丙三台机床各自加工的零件是一等品的事件,那么
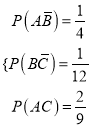 ,即
,即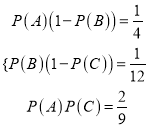 ,解得
,解得![]() ,
,
即分别求甲、乙、丙三台机床各自加工的零件是一等品的概率分别为![]() ,
, ![]() ,
, ![]() .
.
(2)设![]() 为从甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品的事件,则
为从甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品的事件,则![]() ,
,
即从甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品的概率是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
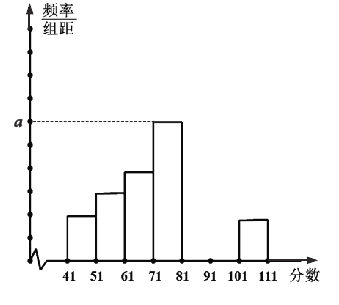
(Ⅰ)完成下面的频率分布表;
(Ⅱ)完成下面的频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;
(Ⅲ)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级某次数学竞赛随机抽取![]() 名学生的成绩,分组为
名学生的成绩,分组为![]() ,统计后得到频率分布直方图如图所示:
,统计后得到频率分布直方图如图所示:
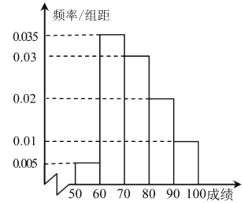
(1)试估计这组样本数据的众数和中位数(结果精确到![]() );
);
(2)年级决定在成绩![]() 中用分层抽样抽取
中用分层抽样抽取![]() 人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在
人组成一个调研小组,对髙一年级学生课外学习数学的情况做一个调查,则在![]() 这三组分別抽取了多少人?
这三组分別抽取了多少人?
(3)现在要从(2)中抽取的![]() 人中选出正副
人中选出正副![]() 个小组长,求成绩在
个小组长,求成绩在![]() 中至少有
中至少有![]() 人当选为正、副小组长的概率.
人当选为正、副小组长的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() ,其中
,其中![]() .
.
(1)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)设![]() (
(![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表和频率分布直方图,回答下面问题:
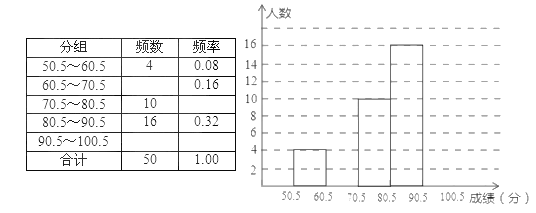
(1)结合图表信息,补全频率分布直方图;
(2)对于参加这次竞赛的900名学生,估计成绩不低于76分的约有多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是某电视台推出的游戏益智节目.选手面对![]() 号
号![]() 扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:
扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:![]() ;
;![]() (单位:岁),其猜对歌曲名称与否人数如图所示.
(单位:岁),其猜对歌曲名称与否人数如图所示.
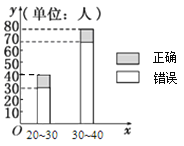
(1)写出![]() 列联表:判断是否有
列联表:判断是否有![]() 的把握认为猜对歌曲名称与否与年龄有关?
的把握认为猜对歌曲名称与否与年龄有关?
说明你的理由.(下面的临界值表供参考)

(2)若某选手能正确回答第一、二、三、四扇门的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,正确回答一个问题后,选择继续回答下一个问题的概率是
,正确回答一个问题后,选择继续回答下一个问题的概率是![]() ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(参考公式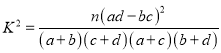 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
, ![]() 是焦点,直线
是焦点,直线![]() 是经过点
是经过点![]() 的任意直线.
的任意直线.
(Ⅰ)若直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且
两点,且![]() (
(![]() 是坐标原点,
是坐标原点, ![]() 是垂足),求动点
是垂足),求动点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若![]() 、
、![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,求证:直线
,求证:直线![]() 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com