
【题目】下列说法正确的个数是( )
①命题“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题
中至少有一个不小于2”的逆命题是真命题
②命题“设![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题
”是一个真命题
③“![]() 的否定是“
的否定是“![]() ”
”
④已知![]() ,
,![]() 都是实数,“
都是实数,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】为降低空气污染,提高环境质量,政府决定对汽车尾气进行整治.某厂家生产甲、乙两种不同型号的汽车尾气净化器,为保证净化器的质量,分别从甲、乙两种型号的净化器中随机抽取100件作为样本进行产品性能质量评估,评估综合得分![]() 都在区间
都在区间![]() .已知评估综合得分与产品等级如下表:
.已知评估综合得分与产品等级如下表:

根据评估综合得分,统计整理得到了甲型号的样本频数分布表和乙型号的样本频率分布直方图(图表如下).


甲型 乙型
(Ⅰ)从厂家生产的乙型净化器中随机抽取一件,估计这件产品为二级品的概率;
(Ⅱ)从厂家生产的乙型净化器中随机抽取3件,设随机变量![]() 为其中二级品的个数,求
为其中二级品的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两种型号汽车尾气净化器的优劣情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为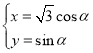 ,其中
,其中![]() 为参数,
为参数,![]() .在以坐标原点
.在以坐标原点![]() 为极点,轴的正半轴为极轴的极坐标系中,点
为极点,轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P—ABCD中,![]() PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.
PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.

(1)求证:MN//平面PAD;
(2)求二面角B—AM—C的大小;
(3)在BC上是否存在点E,使得EN⊥平面AMV?若存在,求![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国际性会议纪念章的一特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向该会议的组织委员会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时,该店一年可销售2000枚,经过市场调研发现,每枚纪念章的销售价格在每枚20元的基础上,每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元(每枚的销售价格应为正整数).
元(每枚的销售价格应为正整数).
(1)写出该特许专营店一年内销售这种纪念章所获得的利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() 的函数关系式;
的函数关系式;
(2)当每枚纪念章销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出这个最大值;
(元)最大,并求出这个最大值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收入
收入![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括①赡养老人费用 ②子女教育费用 ③继续教育费用 ④大病医疗费用
专项附加扣除;(3)专项附加扣除包括①赡养老人费用 ②子女教育费用 ③继续教育费用 ④大病医疗费用![]() 等,其中前两项的扣除标准为:①赡养老人费用:每月共扣除2000元 ②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
等,其中前两项的扣除标准为:①赡养老人费用:每月共扣除2000元 ②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过3000元的部分 | 3% |
2 | 超过3000元至12000元的部分 | 10% |
3 | 超过12000元至25000元的部分 | 20% |
|
|
|
现有李某月收入18000元,膝下有两名子女,需要赡养老人,(除此之外,无其它专项附加扣除,专项附加扣除均按标准的100%扣除),则李某月应缴纳的个税金额为( )
A.590元B.690元C.790元D.890元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.命题“若![]() 则
则![]() ”的逆否命题为真
”的逆否命题为真
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.若命题p为真命题,命题q为假命题,则命题“![]() ”为真命题
”为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com