
【题目】新中国昂首阔步地走进2019年,迎来了她70岁华诞.某平台组织了“伟大的复兴之路一新中国70周年知识问答”活动,规则如下:共有30道单选题,每题4个选项中只有一个正确,每答对一题获得5颗红星,每答错一题反扣2颗红星;若放弃此题,则红星数无变化.答题所获得的红星可用来兑换神秘礼品,红星数越多奖品等级越高.小强参加该活动,其中有些题目会做,有些题目可以排除若干错误选项,其余的题目则完全不会.
(1)请问:对于完全不会的题目,小强应该随机从4个选项中选一个作答,还是选择放弃?(利用统计知识说明理由)
(2)若小强有12道题目会做,剩下的题目中,可以排除一个错误选项、可以排除两个错误选项和完全不会的题目的数量比是![]() .请问:小强在本次活动中可以获得最多红星数的期望是多少?
.请问:小强在本次活动中可以获得最多红星数的期望是多少?
【答案】(1)选择放弃作答;(2)72
【解析】
(1)对于任一道完全不会的题目,若选择放弃,则获得的红星数为0,若选择作答,设小明从四个选项中选一个作答获得的红星数为ξ,ξ取5,-2,列出其分布列,求出期望即可;
(2)依题意,分别求出可以排除一个错误选项、可以排除两个错误选项的每道题目的可获得红星数的期望,由(1)知完全不会的题目可选择放弃,再求每类题目数与该类题目每道题的期望的乘积,最终求和即可得到结果.
(1)对于任一道完全不会的题目,若选择放弃,则获得的红星数为0;
若选择作答,设小明从四个选项中选一个作答获得的红星数为ξ,其分布列为:
ξ | 5 |
|
P |
|
|
所以![]() ,故应该选择放弃作答;
,故应该选择放弃作答;
(2)由题意知,可以排除一个选项的题目有![]() 道,
道,
设这9道题目中每道题小明从四个选项中选一个作答获得的红星数为X,其分布列为:
X | 5 |
|
P |
|
|
所以:![]() ;
;
可以排除两个选项的题目有![]() 道,
道,
设这6道题目中每道题小明从四个选项中选一个作答获得的红星数为Y,其分布列为:
Y | 5 |
|
P |
|
|
![]() ;
;
完全不会的题目有![]() 道,
道,
由(1)知应选择放弃,这3道题中每道题得到的红星数的期望为0.
因此,小明在本次活动中可以获得的最多红星数的期望是:
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为菱形,且
为菱形,且![]() ,
,![]() ,过侧面
,过侧面![]() 中线
中线![]() 的一个平面
的一个平面![]() 与直线
与直线![]() 垂直,并与此四棱锥的面相交,交线围成一个平面图形.
垂直,并与此四棱锥的面相交,交线围成一个平面图形.
(1)画出这个平面图形,并证明![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]()
![]() 的长轴长为4,离心率为
的长轴长为4,离心率为![]() ,点P在椭圆C上.
,点P在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知点M (4,0),点N(0,n),若以PM为直径的圆恰好经过线段PN的中点,求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民月收入总额(工资、薪金等)不超过免征额的部分不必纳税,超过免征额的部分为全月应纳税所得额,个人所得税税款按税率表分段累计计算.为了给公民合理减负,稳步提升公民的收入水平,自2018年10月1日起,个人所得税免征额和税率进行了调整,调整前后的个人所得税税率表如下:

(1)已知小李2018年9月份上交的税费是295元,10月份月工资、薪金等税前收入与9月份相同,请帮小李计算一下税率调整后小李10月份的税后实际收入是多少?
(2)某税务部门在小李所在公司利用分层抽样方法抽取某月100位不同层次员工的税前收入,并制成下面的频率分布直方图.
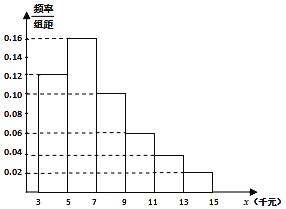
(ⅰ)请根据频率分布直方图估计该公司员工税前收入的中位数;
(ⅱ)同一组中的数据以这组数据所在区间中点的值作代表,按调整后税率表,试估计小李所在的公司员工该月平均纳税多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代社会的竞争,是人才的竞争,各国、各地区、各单位都在广纳贤人,以更好更快的促进国家、地区、单位的发展.某单位进行人才选拔考核,该考核共有三轮,每轮都只设置一个项目问题,能正确解决项目问题者才能进入下一轮考核;不能正确解决者即被淘汰.三轮的项目问题都正确解决者即被录用.已知A选手能正确解决第一、二、三轮的项目问题的概率分别为![]() 、
、![]() 、
、![]() ,且各项目问题能否正确解决互不影响.
,且各项目问题能否正确解决互不影响.
(1)求A选手被淘汰的概率;
(2)设该选手在选拔中正确解决项目问题的个数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,称
,称![]() (其中
(其中![]() )为数列
)为数列![]() 的前k项“波动均值”.若对任意的
的前k项“波动均值”.若对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“趋稳数列”.
为“趋稳数列”.
(1)若数列1,![]() ,2为“趋稳数列”,求
,2为“趋稳数列”,求![]() 的取值范围;
的取值范围;
(2)若各项均为正数的等比数列![]() 的公比
的公比![]() ,求证:
,求证:![]() 是“趋稳数列”;
是“趋稳数列”;
(3)已知数列![]() 的首项为1,各项均为整数,前
的首项为1,各项均为整数,前![]() 项的和为
项的和为![]() . 且对任意
. 且对任意![]() ,都有
,都有![]() , 试计算:
, 试计算:![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .平面
.平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.
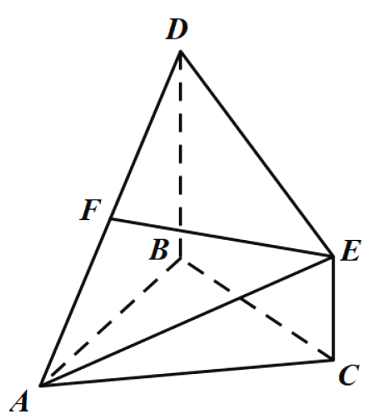
(1)求证:![]() 平面ABC;
平面ABC;
(2)求证:平面![]() 平面ABD.
平面ABD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com