
【题目】如图,在![]() 中,
中,![]() ,点P为
,点P为![]() 的中点,
的中点,![]() 交
交![]() 于点D,现将
于点D,现将![]() 沿
沿![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
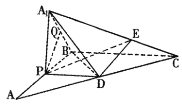
(1)若Q为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点E,使得二面角
上是否存在点E,使得二面角![]() 大小为
大小为![]() .若存在,请求出点E所在位置,若不存在,请说明理由.
.若存在,请求出点E所在位置,若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在;E为线段![]() 的中点
的中点
【解析】
(1)推导出![]() ,
,![]() ,从而
,从而![]() ,推导出
,推导出![]() ,
,![]() ,进而
,进而![]() 平面
平面![]() ,由此能求出
,由此能求出![]() ,
,![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(2)推导出![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,以点
,以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,当点
轴,建立空间直角坐标系,当点![]() 为线段
为线段![]() 的中点时,二面角
的中点时,二面角![]() 的大小为
的大小为![]() .
.
解:(1)证明:在![]() 中,
中,![]() ,
,![]() ,
,
![]() 将
将![]() 沿
沿![]() 翻折至
翻折至![]() ,
,![]() ,
,![]()
又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
在![]() 中
中![]() ,Q为
,Q为![]() 的中点,
的中点,![]() ,
,
又![]() ,
,![]() 平面
平面![]()
(2)![]() 在
在![]() ,
,![]() ,
,![]() ,又
,又![]() 沿
沿![]() 翻折至
翻折至![]() ,
,
且平面![]() 平面
平面![]() ,由(1)有
,由(1)有![]() ,得
,得![]() 平面
平面![]() .
.
以点P为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如图所示.
,如图所示.
则![]() ,
,
![]() .
.
设![]() ,则
,则![]() ,所以
,所以![]()
设平面![]() 的一个法向量为
的一个法向量为![]()
则由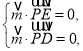 即
即![]()
可得![]()
可取平面![]() 的一个法向量为
的一个法向量为![]()
则 ,解得
,解得![]() .
.
所以当点E为线段![]() 的中点时,二面角
的中点时,二面角![]() 大小为
大小为![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
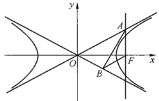
【题目】如图,已知双曲线![]() 的右焦点为F,点A,B分别在C的两条渐近线上,
的右焦点为F,点A,B分别在C的两条渐近线上,![]() 轴,
轴,![]() ,
,![]() (O为坐标原点).
(O为坐标原点).
(1)求双曲线C的方程;
(2)过C上一点![]() 的直线
的直线![]() 与直线AF相交于点M,与直线
与直线AF相交于点M,与直线![]() 相交于点N.证明:当点P在C上移动时,
相交于点N.证明:当点P在C上移动时,![]() 恒为定值,并求此定值.
恒为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015全国高考试题)某公司为了解用户对其产品的满意度,从![]() ,
,![]() 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
![]() 地区:62 73 81 92 95 85 74 64 53 76
地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
![]() 地区:73 83 62 51 91 46 53 73 64 82
地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
根据用户满意度评分,将用户的满意度从低到高分为三个不同等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件![]() :“
:“![]() 地区用户的满意度等级高于
地区用户的满意度等级高于![]() 地区用户的满意度等级”假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求
地区用户的满意度等级”假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.(注:同比是指本期与同期作对比;环比是指本期与上期作对比.如:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比)根据该折线图,下列结论错误的是( )
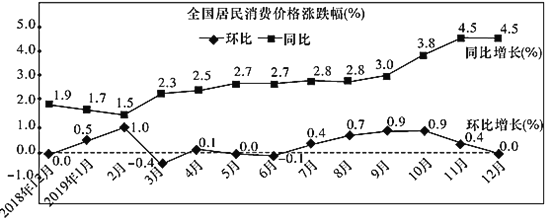
A.2019年12月份,全国居民消费价格环比持平
B.2018年12月至2019年12月全国居民消费价格环比均上涨
C.2018年12月至2019年12月全国居民消费价格同比均上涨
D.2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线C:![]() 1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若
1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若![]() ,则双曲线C的渐近线方程为( )
,则双曲线C的渐近线方程为( )
A.y=±![]() xB.y=±xC.y=±2xD.y=±
xB.y=±xC.y=±2xD.y=±![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线
为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线C有两个不同的交点.
与曲线C有两个不同的交点.
(1)求实数a的取值范围;
(2)已知M为曲线C上一点,且曲线C在点M处的切线与直线![]() 垂直,求点M的直角坐标.
垂直,求点M的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某百货商店今年春节期间举行促销活动,规定消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商店经理对春节前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计,![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(1)经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.请根据上表提供的数据,用最小二乘法求出
具有线性相关关系.请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)该商店规定:若抽中“一等奖”,可领取600元购物券;抽中“二等奖”可领取300元购物券;抽中“谢谢惠顾”,则没有购物券.已知一次抽奖活动获得“一等奖”的概率为![]() ,获得“二等奖”的概率为
,获得“二等奖”的概率为![]() .现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额
.现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: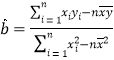 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com