
����Ŀ��(����������12��)
���Ż������Ŀ��ٷ�չ�����ڻ������Ĺ�������Ӧ�˶�����ij�г��о���ԱΪ���˽��������Ӫ��˾![]() �ľ�Ӫ״�����Ըù�˾��������µ��г�ռ���ʽ�����ͳ�ƣ�����������Ӧ������ͼ��
�ľ�Ӫ״�����Ըù�˾��������µ��г�ռ���ʽ�����ͳ�ƣ�����������Ӧ������ͼ��

����������ͼ���Կ������������Իع�ģ������¶��г�ռ����![]() ���·ݴ���
���·ݴ���![]() ֮��Ĺ�ϵ����
֮��Ĺ�ϵ����![]() ����
����![]() �����Իع鷽�̣���Ԥ��
�����Իع鷽�̣���Ԥ��![]() ��˾2017��4�µ��г�ռ���ʣ�
��˾2017��4�µ��г�ռ���ʣ�
����Ϊ��һ�������г�����˾���ٲɹ�һ�����������вɹ��ɱ��ֱ�Ϊ![]() Ԫ/����1200Ԫ/����
Ԫ/����1200Ԫ/����![]() ��
��![]() ����Ϳɹ�ѡ���涨ÿ���������ʹ��4�꣬�����ڶ���ԭ��(������Ƶ�ʵ�)�ᵼ�µ���ʹ������������ͬ�����ǵ���˾��Ӫ�ľ���Ч�棬�ù�˾�����ȶ�������͵ĵ�����100�����п�ѧģ����ԣ��õ������ʹ��������Ƶ�������£�
����Ϳɹ�ѡ���涨ÿ���������ʹ��4�꣬�����ڶ���ԭ��(������Ƶ�ʵ�)�ᵼ�µ���ʹ������������ͬ�����ǵ���˾��Ӫ�ľ���Ч�棬�ù�˾�����ȶ�������͵ĵ�����100�����п�ѧģ����ԣ��õ������ʹ��������Ƶ�������£�
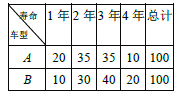
�����㣬ƽ��ÿ������ÿ����Դ�������500Ԫ�������dz��ɹ��ɱ�֮��������ɱ�������ÿ��������ʹ���������������꣬����Ƶ����Ϊÿ������ʹ�������ĸ��ʣ��������![]() ��˾�ĸ����ˣ���ÿ�������������������ֵΪ�������ݣ����ѡ��ɹ��Ŀ�ͣ�
��˾�ĸ����ˣ���ÿ�������������������ֵΪ�������ݣ����ѡ��ɹ��Ŀ�ͣ�
�ο���ʽ���ع�ֱ�߷���Ϊ![]() ������
������ ��
��![]() .
.
���𰸡�����![]() .
.
����Ӧ�òɹ�![]() �.
�.
������������������������������ݣ��ֱ����![]() ��
��![]() �����ù�ʽ�ֱ����
�����ù�ʽ�ֱ����![]() ��
��![]() ��ֵ���ó����Իع鷽�̣�����Ԥ��
��ֵ���ó����Իع鷽�̣�����Ԥ��![]() ��˾2017��4�µ��г�ռ���ʣ������ֱ������Ӧ����ѧ���������ɵó����ۣ�
��˾2017��4�µ��г�ռ���ʣ������ֱ������Ӧ����ѧ���������ɵó����ۣ�
��������������������⣺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
��![]() ��
��
����![]() ʱ��
ʱ��![]() ����Ԥ��
����Ԥ��![]() ��˾2017��4�·�(��
��˾2017��4�·�(��![]() ʱ)���г�ռ����Ϊ
ʱ)���г�ռ����Ϊ![]() .
.
������Ƶ�ʹ��Ƹ��ʣ�ÿ��![]() ���ʹ��1�꣬2�꣬3�꣬4��ĸ��ʷֱ�Ϊ
���ʹ��1�꣬2�꣬3�꣬4��ĸ��ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .
.
��ÿ��![]() ���������ѧ����Ϊ
���������ѧ����Ϊ![]() (Ԫ)��ÿ��
(Ԫ)��ÿ��![]() ���ʹ��1�꣬2�꣬3�꣬4��ĸ��ʷֱ�Ϊ
���ʹ��1�꣬2�꣬3�꣬4��ĸ��ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .
.
��ÿ��![]() ���������ѧ����Ϊ
���������ѧ����Ϊ![]() (Ԫ)
(Ԫ)
��![]()
��Ӧ�òɹ�![]() �.
�.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��һ������
��һ������![]() ����������������һ���˵㹹�ɵȱ������Σ�
����������������һ���˵㹹�ɵȱ������Σ�
����������Բ![]() �ı����̣�
�ı����̣�
������������![]() ��
��![]() ��Ĵ��߽���Բ�ϰ벿���ڵ�
��Ĵ��߽���Բ�ϰ벿���ڵ�![]() ������
������![]() ����Բ
����Բ![]() ����
����![]() ������
������![]() ���ڵ�ֱ�߷ֱ�
���ڵ�ֱ�߷ֱ�![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() Ϊ����������ʱ����ֱ��
Ϊ����������ʱ����ֱ��![]() ��б���Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
��б���Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ�漸���У��б߳�Ϊ![]() ����������������㵽���߾���֮��Ϊ��ֵ
����������������㵽���߾���֮��Ϊ��ֵ![]() ������������⣬�ⳤΪ
������������⣬�ⳤΪ![]() ��������������һ�㵽�ĸ���ľ���֮��Ϊ�� ��
��������������һ�㵽�ĸ���ľ���֮��Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����![]() ΪԲ
ΪԲ![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ��
��![]() ���ϵ�ͶӰΪ
���ϵ�ͶӰΪ![]() ������
������![]() ����
����![]() ������
������![]() �Ĺ켣Ϊ
�Ĺ켣Ϊ![]() .
.
(1)��![]() �ķ��̣�
�ķ��̣�
(2)��![]() ��
��![]() ��������Ľ���Ϊ
��������Ľ���Ϊ![]() ������
������![]() ��ֱ��
��ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ��
��![]() ��
��![]() ������һ��Ϊ
������һ��Ϊ![]() .���Ե�
.���Ե�![]() ΪԲ�ģ����߶�
ΪԲ�ģ����߶�![]() ��Ϊ�뾶��Բ��
��Ϊ�뾶��Բ��![]() ��4�������㣬��
��4�������㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƽ�ָ���Դ�ڹ�Ԫǰ![]() ����ϣ���ıϴ����˹ѧ�ɣ���Ԫǰ
����ϣ���ıϴ����˹ѧ�ɣ���Ԫǰ![]() ���ͣ���ϣ����ѧ��ŷ�����˹��һ��ϵͳ�о�����һ���⣬��Ԫǰ
���ͣ���ϣ����ѧ��ŷ�����˹��һ��ϵͳ�о�����һ���⣬��Ԫǰ![]() ��ǰ��ŷ�����д������ԭ����ʱ������ŷ�����˹���о��ɹ�����һ��ϵͳ�����˻ƽ�ָ��Ϊ������йػƽ�ָ������.�ƽ�ָ���ָ������һ��Ϊ�����ϴ������岿�ֵı�ֵ���ڽ�С������ϴֵı�ֵ�����ֵΪ
��ǰ��ŷ�����д������ԭ����ʱ������ŷ�����˹���о��ɹ�����һ��ϵͳ�����˻ƽ�ָ��Ϊ������йػƽ�ָ������.�ƽ�ָ���ָ������һ��Ϊ�����ϴ������岿�ֵı�ֵ���ڽ�С������ϴֵı�ֵ�����ֵΪ![]() ����
����![]() ��Ϊ�ƽ�ָ���. ��֪˫����
��Ϊ�ƽ�ָ���. ��֪˫����![]() ��ʵ�᳤�뽹��ı�ֵǡ���ǻƽ�ָ�������
��ʵ�᳤�뽹��ı�ֵǡ���ǻƽ�ָ�������![]() ��ֵΪ�� ��
��ֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������f��x����x2��mx��n��m, n��R����
��1����m+n��0�������x�IJ���ʽf��x����x������ú�mʽ�ӱ�ʾ����
��2��������ʵ��m��ʹ�õ�x��[1��2]ʱ������ʽx��f��x����4x���������ʵ��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��ԭ��Ϊ���㣬![]() ���������Ϊ���ᣬ����������ϵ����ֱ֪��
���������Ϊ���ᣬ����������ϵ����ֱ֪��![]() �IJ���������
�IJ��������� (m>0,t����)������
(m>0,tΪ����)������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��
��1����ֱ��![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��������
��������![]() ���ڵ�
���ڵ�![]() ����
����![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ��������������Ͷ����������ÿ��Ͷ�еĸ���Ϊ![]() ����ÿ��Ͷ�еĸ���Ϊ
����ÿ��Ͷ�еĸ���Ϊ![]() ��ÿ�˷ֱ��������Ͷ����
��ÿ�˷ֱ��������Ͷ����
��I���Ǽ�Ͷ�еĴ���Ϊ![]() ����
����![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() ��
��
������������Ͷ��2�εĸ��ʣ�
��������ǡ�ñȼ�Ͷ��2�εĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com