
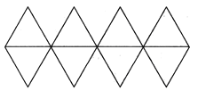
【题目】蹴鞠起源于春秋战国,是现代足球的前身.到了唐代,制作的蹴鞠已接近于现代足球,做法是:用八片鞣制好的尖皮缝制成“圆形”的球壳,在球壳内放一个动物膀胱,“嘘气闭而吹之”,成为充气的球.如图所示,将八个全等的正三角形缝制成一个空间几何体,在几何体内放一个气球,往气球内充气使几何体膨胀,当几何体膨胀成球体(顶点位置不变)且恰好是原几何体外接球时,测得球的体积是![]() ,则正三角形的边长为( )
,则正三角形的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线
轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,写出直线
的极坐标方程化为直角坐标方程,写出直线![]() 的参数方程的标准形式;
的参数方程的标准形式;
(2)已知直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() =x2lnx-a(x2-1)(a∈R),若
=x2lnx-a(x2-1)(a∈R),若![]() ≥0在x∈(0,1] 时恒成立,则实数a的取值范围是
≥0在x∈(0,1] 时恒成立,则实数a的取值范围是
A. [![]() ,+ ∞) B. [
,+ ∞) B. [![]() ,+∞) C. [2,+∞) D. [1,+∞)
,+∞) C. [2,+∞) D. [1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在正四棱锥![]() 中(底面为正方形,顶点在底面上的射影为底面中心的四棱锥),
中(底面为正方形,顶点在底面上的射影为底面中心的四棱锥),![]() ,
,![]() ,侧棱与底面所成角为
,侧棱与底面所成角为![]() ,侧面与底面所成角为
,侧面与底面所成角为![]() ,侧面等腰三角形的底角为
,侧面等腰三角形的底角为![]() ,相邻两侧面的二面角为
,相邻两侧面的二面角为![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com