

(1)证明PA⊥平面ABCD,PB∥平面EAC;
(2)求以AC为棱,EAC与DAC为面的二面角θ的正切值.
(1)证法一:因为底面ABCD是菱形,∠ABC=60°,
所以AB=AD=AC=a.在△PAB中,有PA2+AB2=2a2=PB2.
同理,PA⊥AD,所以PA⊥平面ABCD.
因为![]() =
=![]() +
+![]() +
+![]() =2
=2![]() +
+![]() +
+![]() =(
=(![]() +
+![]() )+(
)+(![]() +
+![]() )=
)=![]() +
+![]() .
.
所以![]() 、
、![]() 、
、![]() 共面.又PB
共面.又PB![]() 平面EAC,所以PB∥平面EAC.
平面EAC,所以PB∥平面EAC.
证法二:同证法一得PA⊥平面ABCD.
连结BD,设BD∩AC=O,则O为BD的中点.

连结OE,因为E是PD的中点,所以PB∥OE.
又PB![]() 平面EAC,OE
平面EAC,OE![]() 平面EAC.故PB∥平面EAC.
平面EAC.故PB∥平面EAC.
(2)解:作EG∥PA交AD于点G,由PA⊥平面ABCD,
知EG⊥平面ABCD,
作GH⊥AC于点H,连结EH,则EH⊥AC,∠EHG即为二面角θ的平面角.
又E是PD的中点,从而G是AD的中点,
EG=![]() a,AG=
a,AG=![]() a,GH=AGsin60°=
a,GH=AGsin60°=![]() a.所以tanθ=
a.所以tanθ=![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:
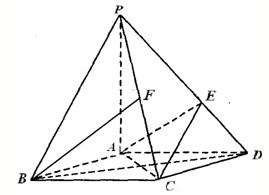 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2| 2 |
| PE |
| PD |
| π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com