在考试测评中.常用难度曲线图来检测题目的质量.一般来说.全卷得分高的学生.在某道题目上的答对率也应较高.如果是某次数学测试压轴题的第1.2问得分难度曲线图.第1.2问满分均为6分.图中横坐标为分数段.纵坐标为该分数段的全体考生在第1.2问的平均难度.则下列说法正确的是( )A．此题没有考生得12分B．此题第1问比第2问更能区分学生数学成绩的好与坏C 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

9．在考试测评中，常用难度曲线图来检测题目的质量，一般来说，全卷得分高的学生，在某道题目上的答对率也应较高，如果是某次数学测试压轴题的第1、2问得分难度曲线图，第1、2问满分均为6分，图中横坐标为分数段，纵坐标为该分数段的全体考生在第1、2问的平均难度，则下列说法正确的是（　　）

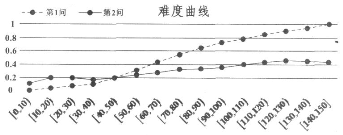
	A．	此题没有考生得12分
	B．	此题第1问比第2问更能区分学生数学成绩的好与坏
	C．	分数在[40，50）的考生此大题的平均得分大约为4.8分
	D．	全体考生第1问的得分标准差小于第2问的得分标准差

分析由图中横坐标为分数段，纵坐标为该分数段的全体考生在第1、2问的平均难度，分数越高的同学，第1问得分高，说明此题第1问比第2问更能区分学生数学成绩的好与坏，即可得出结论．

解答解：由图中横坐标为分数段，纵坐标为该分数段的全体考生在第1、2问的平均难度，分数越高的同学，
第1问得分高，说明此题第1问比第2问更能区分学生数学成绩的好与坏，
故选B．

点评本题考查难度曲线图，考查数形结合的数学思想，考查学生分析解决问题的能力，属于中档题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

19．设A={4，5，6，7}，B={x∈N|3≤x＜6}，则A∩B=（　　）

A．

{4，5，6}

B．

{4，5}

C．

{3，4，5}

D．

{5，6，7}

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

20．函数f（x）=x²-2x+2在（-∞，1）上的反函数f^-1（x）=1-$\sqrt{x-1}$．x＞1．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

17．对具有线性相关关系的变量x，y，测得一组数据如下

x	1	2	3	4
y	4.5	4	3	2.5

根据表，利用最小二乘法得到它的回归直线方程为（　　）

A．

y=-0.7x+5.20

B．

y=-0.7x+4.25

C．

y=-0.7x+6.25

D．

y=-0.7x+5.25

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．

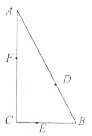如图，某公园有三条观光大道AB，BC，AC围成直角三角形，其中直角边BC=200m，斜边AB=400m，现有甲、乙、丙三位小朋友分别在AB，BC，AC大道上嬉戏，所在位置分别记为点D，E，F．
（1）若甲、乙都以每分钟100m的速度从点B出发在各自的大道上奔走，到大道的另一端时即停，乙比甲迟2分钟出发，当乙出发1分钟后，求此时甲乙两人之间的距离；
（2）设∠CEF=θ，乙丙之间的距离是甲乙之间距离的2倍，且∠DEF=$\frac{π}{3}$，请将甲乙之间的距离y表示为θ的函数，并求甲乙之间的最小距离．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．已知0＜x＜$\frac{π}{2}$，且tan（x-$\frac{π}{4}$）=-$\frac{1}{7}$，则sinx+cosx=$\frac{7}{5}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．在极坐标系中，射线l：θ=$\frac{π}{6}$与圆C：ρ=2交于点A，椭圆Γ的方程为ρ²=$\frac{3}{1+2si{n}^{2}θ}$，以极点为原点，极轴为x轴正半轴建立平面直角坐标系xOy
（Ⅰ）求点A的直角坐标和椭圆Γ的参数方程；
（Ⅱ）若E为椭圆Γ的下顶点，F为椭圆Γ上任意一点，求$\overrightarrow{AE}$•$\overrightarrow{AF}$的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

18．