已知向量a,b是平面α内的一组基底,向量c=a+2b,对于平面α内异于a,b的不共线向量m,n,现给出下列命题:
①当m,n分别与a,b对应共线时,满足c=m+2n的向量m,n有无数组;
②当m,n与a,b均不共线时,满足c=m+2n的向量m,n有无数组;
③当m,n分别与a,b对应共线时,满足c=m+2n的向量m,n不存在;
④当m与a共线,但向量n与向量b不共线时,满足c=m+2n的向量m,n有无数组.
其中真命题的序号是________.(填上所有真命题的序号)
②③④
分析:根据题意,分析命题:利用平面向量的基本定理,同一个向量在两个方向上的分解是唯一的,判断出①③的对错;对于③④,由于基底的方向可以是任意的,所以对同一个向量分解唯一时,对应的基底可无数个,综合可得答案.
解答:对应①,由平面向量基本定理,向量分解是唯一的;所以只有
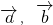
满足
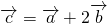
,不在存在

故①错;
对于②,由于

方向任意,所以满足

的向量

有无数组,故②对;
对于③由①的判断过程得到③对;
对于④,由于
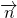
向量的任意性,故可构成不同的基底;所以满足

的向量

有无数组,故④对
故答案为:②③④
点评:本题考查当基底的方向确定,则对于一个向量的分解是唯一的;当基底方向不确定,对于一个向量的分解系数确定,则基底无数个.

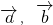 满足
满足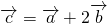 ,不在存在
,不在存在 故①错;
故①错; 方向任意,所以满足
方向任意,所以满足 的向量
的向量 有无数组,故②对;
有无数组,故②对; 向量的任意性,故可构成不同的基底;所以满足
向量的任意性,故可构成不同的基底;所以满足 的向量
的向量 有无数组,故④对
有无数组,故④对

![]() B.5
B.5![]() C.10 D.5
C.10 D.5