
分析 利用柯西不等式的变形:设a1,a2,…an为实数,b1,b2,…bn为正数,则$\frac{{{a}_{1}}^{2}}{{b}_{1}}$+$\frac{{{a}_{2}}^{2}}{{b}_{2}}$+…+$\frac{{{a}_{n}}^{2}}{{b}_{n}}$≥$\frac{({a}_{1}+{a}_{2}+…+{a}_{n})^{2}}{{b}_{1}+{b}_{2}+…+{b}_{n}}$当且仅当$\frac{{a}_{1}}{{b}_{1}}$=$\frac{{a}_{2}}{{b}_{2}}$=…=$\frac{{a}_{n}}{{b}_{n}}$时取等号,计算即得结论.
解答 解:$\frac{{{a}_{1}}^{2}}{2+{a}_{1}}$+$\frac{{{a}_{2}}^{2}}{2+{a}_{2}}$+…$\frac{{{a}_{2013}}^{2}}{2+{a}_{2013}}$+$\frac{{{a}_{2014}}^{2}}{2+{a}_{2014}}$≥$\frac{({a}_{1}+{a}_{2}+…+{a}_{2014})^{2}}{2×2014+({a}_{1}+{a}_{2}+…+{a}_{2014})}$=$\frac{1}{4028+1}$=$\frac{1}{4029}$,
当且仅当$\frac{{a}_{1}}{2+{a}_{1}}$=$\frac{{a}_{2}}{2+{a}_{2}}$=…=$\frac{{a}_{2014}}{2+{a}_{2014}}$取等号,
故答案为:$\frac{1}{4029}$.
点评 本题考查柯西不等式的变形,注意解题方法的积累,属于中档题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,1+2$\sqrt{2}$] | B. | [1-2$\sqrt{2}$,1+2$\sqrt{2}$] | C. | [1-2$\sqrt{2}$,3] | D. | [1-$\sqrt{2}$,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<λ<1 | B. | λ=0 | C. | λ<0且λ≠-1 | D. | λ≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
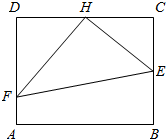 某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com