
分析 由等差数列的通项公式求出首项和公差,然后利用前n项和公式求出含有绝对值的项的和Tn即可.
解答 解:设等差数列{an}的前n项和为Sn,
∵an=10-3n,∴数列的首项为a1=7,公差为d=-3,
∴a3=1>0,a4=-2<0;
∴该数列的前n项和为
Sn=na1+$\frac{n(n-1)}{2}$=7n-$\frac{3}{2}$n(n-1)=-$\frac{3}{2}$n2+$\frac{17}{2}$n;
当n≤3时,|a1|+|a2|+…|an|=Sn=-$\frac{3}{2}$n2+$\frac{17}{2}$n;
当n>3时,|a1|+|a2|+…+|an|=-Sn+2S3=$\frac{3}{2}$n2-$\frac{17}{2}$n+24;
即Tn=|a1|+|a2|+|a3|+…+|an|
=$\left\{\begin{array}{l}{-{\frac{3}{2}n}^{2}+\frac{17}{2}n,n≤3}\\{{\frac{3}{2}n}^{2}-\frac{17}{2}n+24,n>3}\end{array}\right.$.
点评 本题考查了等差数列的通项公式与前n项和公式的应用问题,也考查了绝对值的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|-1≤y≤3} | B. | {-3,-1,1,3} | C. | {y|-3≤y≤3} | D. | {-1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
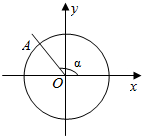 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的坐标是(cosα,$\frac{3}{5}$),则cosα-sinα=$-\frac{7}{5}$.
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的坐标是(cosα,$\frac{3}{5}$),则cosα-sinα=$-\frac{7}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+2$\sqrt{2}$ | B. | 4+2$\sqrt{3}$ | C. | 4+2$\sqrt{6}$ | D. | 6+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com