
分析 |$\overrightarrow{a}$-t$\overrightarrow{e}$|≥|$\overrightarrow{a}$-$\overrightarrow{e}$|,且$\overrightarrow{a}$≠$\overrightarrow{e}$,两边平方化为t2-$2t\overrightarrow{a}•\overrightarrow{e}$+$2\overrightarrow{a}•\overrightarrow{e}$-1≥0恒成立,可得△≤0,解出即可.
解答 解:∵|$\overrightarrow{a}$-t$\overrightarrow{e}$|≥|$\overrightarrow{a}$-$\overrightarrow{e}$|,且$\overrightarrow{a}$≠$\overrightarrow{e}$,
∴${\overrightarrow{a}}^{2}-2t\overrightarrow{a}•\overrightarrow{e}$+${t}^{2}{\overrightarrow{e}}^{2}$≥${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{e}$+${\overrightarrow{e}}^{2}$,
化为t2-$2t\overrightarrow{a}•\overrightarrow{e}$+$2\overrightarrow{a}•\overrightarrow{e}$-1≥0恒成立,
∴△=$4(\overrightarrow{a}•\overrightarrow{e})^{2}$-4($2\overrightarrow{a}•\overrightarrow{e}$-1)≤0,
化为$(\overrightarrow{a}•\overrightarrow{e}-1)^{2}≤$0,
∴$\overrightarrow{a}$•$\overrightarrow{e}$=1.
点评 本题考查了向量数量积运算性质、二次函数的性质、一元二次不等式的解集与判别式的关系,考查了推理能力与计算能力,属于中档题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
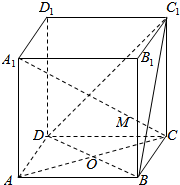 已知在正方体ABCD-A1B1C1D1中,O是DB的中点,直线A1C交平面C1BD于点M,判断下列结论是否正确:
已知在正方体ABCD-A1B1C1D1中,O是DB的中点,直线A1C交平面C1BD于点M,判断下列结论是否正确:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com